
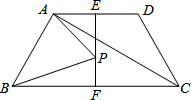
 如图,在等腰梯形ABCD中,∠BCD=60°,AD=2,对角线AC平分∠BCD,E、F分别是底边AD、BC的中点,连接EF,点P是EF上的任意一点,连接PA、PB,则PA+PB的最小值为2$\sqrt{3}$.
如图,在等腰梯形ABCD中,∠BCD=60°,AD=2,对角线AC平分∠BCD,E、F分别是底边AD、BC的中点,连接EF,点P是EF上的任意一点,连接PA、PB,则PA+PB的最小值为2$\sqrt{3}$. 分析 要求PA+PB的最小值,PA、PB不能直接求,可考虑转化PA、PB的值,从而找出其最小值求解.
解答 解:连接PC.
∵E,F分别是底边AD,BC的中点,四边形ABCD是等腰梯形,
∴B点关于EF的对称点C点,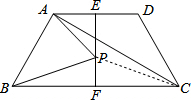
∴AC即为PA+PB的最小值,
∵∠BCD=60°,对角线AC平分∠BCD,
∴∠ABC=60°,∠BCA=30°,
∴∠BAC=90°,
∵AD=2,
∴PA+PB的最小值=AB•tan60°=2$\sqrt{3}$.
故答案为:2$\sqrt{3}$.
点评 本题考查了等腰梯形的性质和轴对称等知识的综合应用、两点之间线段最短等知识,解题的关键是学会利用对称解决最短问题,属于中考常考题型.


 口算能手系列答案
口算能手系列答案科目:初中数学 来源: 题型:解答题
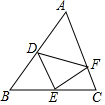 如图,设△ABC的面积为1,点D,E,F分别在AB,BC,CA上,AD=$\frac{1}{m}$AB,BE=$\frac{1}{n}$BC,CF=$\frac{1}{p}$CA,且满足m+n+p=9,m2+n2+p2=29.m3+n3+p3=99,求△DEF的面积.
如图,设△ABC的面积为1,点D,E,F分别在AB,BC,CA上,AD=$\frac{1}{m}$AB,BE=$\frac{1}{n}$BC,CF=$\frac{1}{p}$CA,且满足m+n+p=9,m2+n2+p2=29.m3+n3+p3=99,求△DEF的面积.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 填空:把下面的推里过程补充完整,并在括号内注明理由.
填空:把下面的推里过程补充完整,并在括号内注明理由.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 0.765×105 | B. | 7.65×104 | C. | 76.5×103 | D. | 7.65×105 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 已知三条线段h,m,c,求作△ABC,使其BC边上的高AH=h,中线AD=m,AB=c.
已知三条线段h,m,c,求作△ABC,使其BC边上的高AH=h,中线AD=m,AB=c.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com