
(1)解:过D作DF⊥BC于F,
∵AD∥BC,∠ABC=90°,
∴AD和BC为⊙O的切线,
而CD为⊙O的切线,
∴DE=DA=x,CE=CB=y,
而DF=AB=8,FC=y-x,
∴(x+y)
2=8
2+(x-y)
2,
∴y=
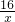
;

(2)证明:连AE,
∵AB为直径,
∴∠AEB=90°,
而DA=DE,
∴∠DAE=∠DEA,
而∠DAE+∠F=∠DEA+∠DEF=90°,
∴∠F=∠DEF,
∴DE=DF,
∴AD=

AF;
(3)解:当0<t≤2,
∵DQ=t,BP=t,
∴当AQ=BP时,∠MQD=90°,
∴t+t=2,
∴t=1;
当2<t≤8,
若∠QDM=90°,如图,
∴∠AQD=∠C,
∴Rt△AQD∽Rt△PCM,
∴AD:PM=AQ:PC,即AD:AQ=PM:PC,
而PM:PC=DF:FC=8:6=4:3,
∵AQ=t-2,
∴2:(t-2)=4:3,
∴t=

;
若∠QMD=90°,如图,
过M作MH⊥AB,

∴∠HQM=∠C,
∴Rt△HQM∽Rt△PCM,
∴MH:MP=HQ:PC,即HM:HQ=MP:PC,
∴HM:HQ=MP:PC=DF:FC=4:3,
PC=8-t,PM=

(8-t),
而MH=t,QH=BH-BQ=

(8-t)-(10-t)=

-

t,
∴t:(

-

t)=4:3,
∴t=
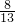
<2,舍去.

当∠DQM=90°,如图,
过M作MH⊥AB于H点,则PM=

(8-t),MN=t,AQ=t-2,
∴QH=8-(t-2)-

(8-t)=

t-

,
∴Rt△AQD∽Rt△HMQ,
∴AD:QH=AQ:HM,即2:(

t-

)=(t-2):t,
∴t
2-10t+4=0,t=5±

,
∴t=5+

>8(舍).
分析:(1)过D作DF⊥BC于F,根据切线长定理得到DE=DA=x,CE=CB=y,在Rt△DFC中,利用勾股定理即可得到x,y的关系;
(2)连AE,根据直径所对的圆周角为直角得到∠AEB=90°,而DA=DE,得到∠DAE=∠DEA,根据等角的余角相等得到∠F=∠DEF,则DE=EF,即可得到结论;
(3)分类讨论:当0<t≤2,当AQ=BP时,∠MQD=90°;当2<t≤8,分若∠QDM=90°,或∠QMD=90°,或∠DQM=90°进行讨论,构建三角形相似列出t的方程求解.
点评:本题考查了三角形相似的判定与性质;也考查了直角梯形的性质和切线的性质以及分类讨论思想的运用.

 AF;
AF;
 (1)解:过D作DF⊥BC于F,
(1)解:过D作DF⊥BC于F,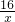 ;
;
 AF;
AF; ;
;
 (8-t),
(8-t), (8-t)-(10-t)=
(8-t)-(10-t)= -
- t,
t, -
- t)=4:3,
t)=4:3,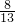 <2,舍去.
<2,舍去.
 (8-t),MN=t,AQ=t-2,
(8-t),MN=t,AQ=t-2, (8-t)=
(8-t)= t-
t- ,
, t-
t- )=(t-2):t,
)=(t-2):t, ,
, >8(舍).
>8(舍).

 应用题点拨系列答案
应用题点拨系列答案 状元及第系列答案
状元及第系列答案 同步奥数系列答案
同步奥数系列答案 如图,在梯形ABCD中,AD∥BC,BC=30cm,动点M从A点开始沿AD边向D以1cm/s的速度运动,动点N从C点开始沿CB边向B以3cm/s的速度运动,M、N分别从A、C同时出发,当其中一点到端点时,另一点也随之停止运动,设运动时间为t s,t为何值时,四边形ABNM是平行四边形?
如图,在梯形ABCD中,AD∥BC,BC=30cm,动点M从A点开始沿AD边向D以1cm/s的速度运动,动点N从C点开始沿CB边向B以3cm/s的速度运动,M、N分别从A、C同时出发,当其中一点到端点时,另一点也随之停止运动,设运动时间为t s,t为何值时,四边形ABNM是平行四边形?