
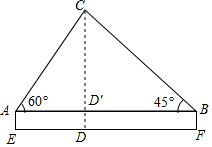
 从相距100m的A,B两点观侧建筑物CD,用测角仪测得建筑物顶点CA体的高度的仰角分别为60°和45°,求E,F两点到建筑物底端D的距离分别为多少米.
从相距100m的A,B两点观侧建筑物CD,用测角仪测得建筑物顶点CA体的高度的仰角分别为60°和45°,求E,F两点到建筑物底端D的距离分别为多少米. 分析 直接根据题意表示出AD′,BD′的长,进而利用已知求出答案.
解答 解:设AD′=xm,
∵∠CAD′=60°,
∴CD′=$\sqrt{3}$xm,
∵∠CBD′=45°,
∴CD′=BD′,
∴BD′=$\sqrt{3}$xm,
则AB=EF=x+$\sqrt{3}$x=100,
解得:x=50($\sqrt{3}$-1),
故DF=BD′=$\sqrt{3}$×50($\sqrt{3}$-1)=(150-50$\sqrt{3}$)m,
答:E点到D点距离为:50($\sqrt{3}$-1)m,F到D点距离为:(150-50$\sqrt{3}$)m.
点评 此题主要考查了解直角三角形的应用,正确用未知数表示出AD′,BD′的长是解题关键.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:解答题
 作图并回答问题:
作图并回答问题:查看答案和解析>>
科目:初中数学 来源: 题型:选择题
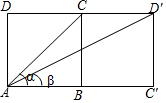 如图,已知正方形ABCD的边长为1,若将边BC绕点B旋转90°后,得到正方形BC′D′C,连接AC、AD′,设∠BAC=α∠C′AD′=β,那么sinα+sinβ等于( )
如图,已知正方形ABCD的边长为1,若将边BC绕点B旋转90°后,得到正方形BC′D′C,连接AC、AD′,设∠BAC=α∠C′AD′=β,那么sinα+sinβ等于( )| A. | $\frac{3}{2}$ | B. | $\sqrt{2}$+$\sqrt{5}$ | C. | $\frac{{\sqrt{2}+\sqrt{5}}}{10}$ | D. | $\frac{{5\sqrt{2}+2\sqrt{5}}}{10}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
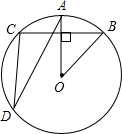 如图,在⊙O中,弦BC=8cm,OA⊥BC,与⊙O交于点A,OA=4$\sqrt{2}$cm
如图,在⊙O中,弦BC=8cm,OA⊥BC,与⊙O交于点A,OA=4$\sqrt{2}$cm查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com