
分析 首先由①③消去z,得出关于x、y的二元一次方程与②组成二元一次方程组,求得x、y,进一步代入①求得z得出答案即可.
解答 解:$\left\{\begin{array}{l}{x+3y+2z=2,①}\\{2x-y=7,②}\\{3x+2y-4z=3.③}\end{array}\right.$
①×2+③得:5x+8y=7,④
②④组成方程组得$\left\{\begin{array}{l}{2x-y=7}\\{5x+8y=7}\end{array}\right.$
解得:$\left\{\begin{array}{l}{x=3}\\{y=-1}\end{array}\right.$
代入①得3+3×(-1)+2z=2,
解得:z=1,
所以原方程组的解为$\left\{\begin{array}{l}{x=3}\\{y=-1}\\{z=1}\end{array}\right.$.
点评 此题考查三元一次方程组的解法,掌握逐步消元的方法是解决问题的关键.


 互动课堂系列答案
互动课堂系列答案 激活思维智能训练课时导学练系列答案
激活思维智能训练课时导学练系列答案科目:初中数学 来源: 题型:选择题
| A. | 图象经过点(-1,-2) | B. | 图象不经过第一象限 | ||
| C. | 图象与y轴交点坐标是(0,-1) | D. | y的值随x值的增大而增大 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
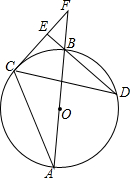 AB为⊙O的直径,C,D为⊙O上不同于A,B的两点,∠ABD=2∠BAC,连接CD,过点C作CE⊥DB,垂足为E,直径AB与CE的延长线相交于F点.
AB为⊙O的直径,C,D为⊙O上不同于A,B的两点,∠ABD=2∠BAC,连接CD,过点C作CE⊥DB,垂足为E,直径AB与CE的延长线相交于F点.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
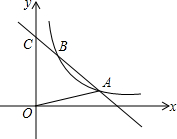 如图,一次函数的图象与y轴交于C(0,4),且与反比例函数y=$\frac{k}{x}$(x>0)的图象在第一象限内交于A(3,a),B(1,b)两点,
如图,一次函数的图象与y轴交于C(0,4),且与反比例函数y=$\frac{k}{x}$(x>0)的图象在第一象限内交于A(3,a),B(1,b)两点,查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com