
 右、C在左).
右、C在左).| 5 |
| 5 |
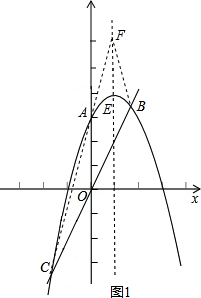 解:(1)点A(0,2m-7)代入y=-x2+2x+m-2,
解:(1)点A(0,2m-7)代入y=-x2+2x+m-2,
|
|
|
| 3 |
| 3 |
| 3 |
| 3 |
| 3 |
| 3 |
| 3 |
| 3 |
|
|
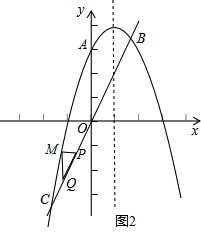
| 3 |
| 3 |
|
|
-1±
| ||
| 4 |
| 3 |
-1+
| ||
| 4 |
| 3 |


科目:初中数学 来源: 题型:
查看答案和解析>>
科目:初中数学 来源: 题型:
 (2012•石景山区二模)如图所示,圆圈内分别标有1,2,…,12,这12个数字,电子跳蚤每跳一步,可以从一个圆圈逆时针跳到相邻的圆圈,若电子跳蚤所在圆圈的数字为n,则电子跳蚤连续跳(3n-2)步作为一次跳跃,例如:电子跳蚤从标有数字1的圆圈需跳3×1-2=1步到标有数字2的圆圈内,完成一次跳跃,第二次则要连续跳3×2-2=4步到达标有数字6的圆圈,…依此规律,若电子跳蚤从①开始,那么第3次能跳到的圆圈内所标的数字为
(2012•石景山区二模)如图所示,圆圈内分别标有1,2,…,12,这12个数字,电子跳蚤每跳一步,可以从一个圆圈逆时针跳到相邻的圆圈,若电子跳蚤所在圆圈的数字为n,则电子跳蚤连续跳(3n-2)步作为一次跳跃,例如:电子跳蚤从标有数字1的圆圈需跳3×1-2=1步到标有数字2的圆圈内,完成一次跳跃,第二次则要连续跳3×2-2=4步到达标有数字6的圆圈,…依此规律,若电子跳蚤从①开始,那么第3次能跳到的圆圈内所标的数字为查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com