
在Rt△ABC中,∠ACB=90°,∠A=30°,BD是△ABC的角平分线, DE⊥AB于点E.
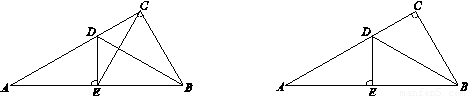
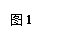
(1)如图1,连接EC,求证:△EBC是等边三角形;
(2)点M是线段CD上的一点(不与点C,D重合),以BM为一边,在BM的下方作∠BMG=60°,MG交DE延长线于点G.请你在图2中画出完整图形,并直接写出MD,DG与AD之间的数量关系;
(3)如图3,点N是线段AD上的一点,以BN为一边,在BN的下方作∠BNG=60°,NG交DE延长线于点G,且MB=MG.试探究ND,DG与AD数量之间的关系,并说明理由.
(1)证明:在Rt△ABC中,∠ACB=90°,∠A=30°,∴ ,
, ,∵BD平分∠ABC,∴
,∵BD平分∠ABC,∴ ,∴
,∴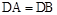 ,∵DE⊥AB于点E,∴
,∵DE⊥AB于点E,∴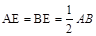 ,∴
,∴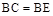 ,∴△BCE是等边三角形
,∴△BCE是等边三角形
(2)AD = DG+DM

(3)AD = DG-DN
【解析】
试题分析:(1)要证明△BCE是等边三角形,首先要知道BC和BE相等,由于已给出 ,所以要证明
,所以要证明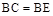 ,只需证明
,只需证明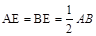 ,利用题目中给出的数据,可以很容易求出。(2)由于
,利用题目中给出的数据,可以很容易求出。(2)由于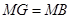 ,且
,且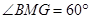 ,所以△MGB是等边三角形,做GF交DB于点F,所以△DFG为等边三角形,所以
,所以△MGB是等边三角形,做GF交DB于点F,所以△DFG为等边三角形,所以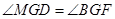 ,又
,又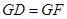 ,
, ,所以△MDG≌△BFG,所以
,所以△MDG≌△BFG,所以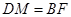 ,又
,又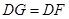 ,
,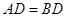 ,而
,而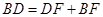 ,所以
,所以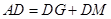
(3)延长BD至H,使得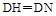 ,由(1)得
,由(1)得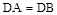 ,
,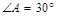 ,∵DE⊥AB于点E,∴
,∵DE⊥AB于点E,∴ ,∴
,∴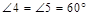 ,∴△NDH是等边三角形,∴
,∴△NDH是等边三角形,∴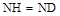 ,
,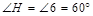 ,∴
,∴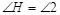 ,∵
,∵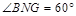 ,∴
,∴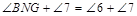 ,即
,即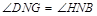 ,在△DNG和△HNB中,
,在△DNG和△HNB中,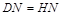 ,
,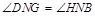 ,
,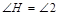 ,∴△DNG≌△HNB,∴DG=HB,∵HB=HD+DB=ND+AD,∴DG= ND+AD,∴AD = DG-ND
,∴△DNG≌△HNB,∴DG=HB,∵HB=HD+DB=ND+AD,∴DG= ND+AD,∴AD = DG-ND
考点:其中一个锐角为30度的直角三角形的特殊性
点评:本题较为复杂,第一问通过直角三角形的特殊性,可以较容易解出来


湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com