

 解:(1)在Rt△OBA中,∠AOB=30°,AB=3,
解:(1)在Rt△OBA中,∠AOB=30°,AB=3, =
= ,
, =3
=3 ,
, ).
). (k≠0).
(k≠0). =
= ,k=9
,k=9 .
. .
. ,sin30°=
,sin30°= ,
, .
. ,
, •
• .
.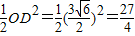 .
. .
.

科目:初中数学 来源: 题型:
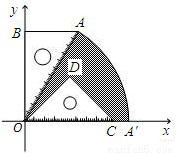
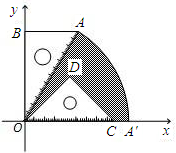 已知:如图,有一块含30°的直角三角板OAB的直角边长BO的长恰与另一块等腰直角三角板ODC的斜边OC的长相等,把该套三角板放置在平面直角坐标系中,且AB=3.
已知:如图,有一块含30°的直角三角板OAB的直角边长BO的长恰与另一块等腰直角三角板ODC的斜边OC的长相等,把该套三角板放置在平面直角坐标系中,且AB=3.查看答案和解析>>
科目:初中数学 来源: 题型:
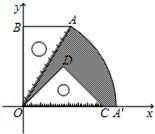 已知:如图,有一块含30°角的直角三角板OAB的直角边BO的长恰与另一块等腰直角三角板ODC的斜边OC的长相等,把该套三角板放置在平面直角坐标系中,AB=
已知:如图,有一块含30°角的直角三角板OAB的直角边BO的长恰与另一块等腰直角三角板ODC的斜边OC的长相等,把该套三角板放置在平面直角坐标系中,AB=| 3 |
查看答案和解析>>
科目:初中数学 来源:2011-2012学年河北省石家庄市外国语学校九年级(上)第三阶段数学试卷(解析版) 题型:解答题
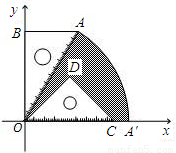
查看答案和解析>>
科目:初中数学 来源:2011年内蒙古通辽市九校联合中考数学模拟试卷(解析版) 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com