
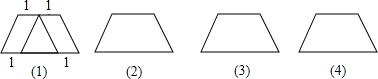
 优生乐园系列答案
优生乐园系列答案科目:初中数学 来源: 题型:
查看答案和解析>>
科目:初中数学 来源: 题型:
查看答案和解析>>
科目:初中数学 来源: 题型:059
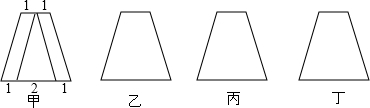
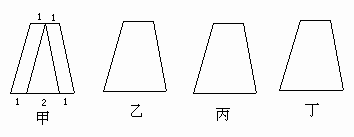
如图所示,甲是把一个上底等于2,下底等于4的等腰梯形纸片裁成面积相等的三块的一种方案.请在乙、丙、丁中用三种不同的方法进行裁剪(必要时须标明相关的数量或辅助线).
查看答案和解析>>
科目:初中数学 来源: 题型:044
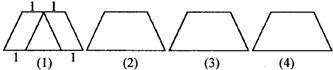
如图所示,是把一个上底等于2,下底等于4的等腰梯形纸片截成面积相等的三块的一种方案,请将下面另外三个和该梯形完全一样的图形,用三种不同的方法进行裁剪,使其分别裁剪为面积相等的三块.(必要时应在图上表出数据)
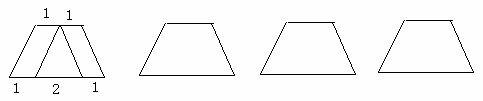
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com