
| 1 |
| x |
| 1 |
| 3 |
| 1 |
| a |
| 1 |
| b |
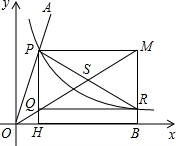 ∠MOB=
∠MOB=| 1 |
| 3 |
| 1 |
| a |
| 1 |
| b |
| 1 |
| a |
| 1 |
| a |
| 1 |
| ab |
| 1 |
| ab |
| 1 |
| b |
| 1 |
| ab |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 3 |


 期末宝典单元检测分类复习卷系列答案
期末宝典单元检测分类复习卷系列答案科目:初中数学 来源: 题型:
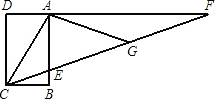 “三等分一个角”是数学史上一个著名问题.今天人们已经知道,仅用圆规和直尺是不可能作出的,在探索中,有人曾利用过如下的图形:其中,ABCD是长方形,F是DA延长线上一点,G是CF上一点,并且∠ACG=∠AGC,∠GAF=∠GFA,你能证明∠ECB=
“三等分一个角”是数学史上一个著名问题.今天人们已经知道,仅用圆规和直尺是不可能作出的,在探索中,有人曾利用过如下的图形:其中,ABCD是长方形,F是DA延长线上一点,G是CF上一点,并且∠ACG=∠AGC,∠GAF=∠GFA,你能证明∠ECB=| 1 | 3 |
查看答案和解析>>
科目:初中数学 来源: 题型:
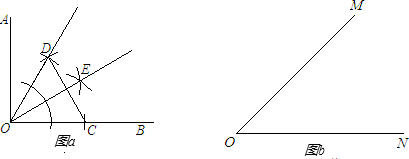
| 1 |
| x |
| 1 |
| 3 |
| 1 |
| a |
| 1 |
| b |
| 1 |
| 3 |
查看答案和解析>>
科目:初中数学 来源: 题型:
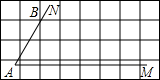 (2012•天津)“三等分任意角”是数学史上一个著名问题.已知一个角∠MAN,设∠α=
(2012•天津)“三等分任意角”是数学史上一个著名问题.已知一个角∠MAN,设∠α=| 1 | 3 |
查看答案和解析>>
科目:初中数学 来源:2011年江苏省无锡市育才中学中考数学二模试卷(解析版) 题型:解答题

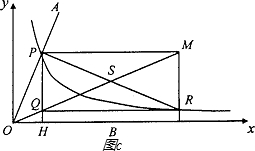
 的图象交于点P,以P为圆心、2OP长为半径作弧交图象于点R.分别过点P和R作x轴和y轴的平行线,两直线相交于点M,连接OM得到∠MOB,则∠MOB=
的图象交于点P,以P为圆心、2OP长为半径作弧交图象于点R.分别过点P和R作x轴和y轴的平行线,两直线相交于点M,连接OM得到∠MOB,则∠MOB= ∠AOB.要明白帕普斯的方法,请研究以下问题:
∠AOB.要明白帕普斯的方法,请研究以下问题: )、R(b,
)、R(b, ),求直线OM对应的函数关系式(用含a、b的代数式表示).
),求直线OM对应的函数关系式(用含a、b的代数式表示). ∠AOB.
∠AOB.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com