如图，菱形ABCD中，对角线AC、BD相交于点O，AC=6，BD=8．点E为AD边上一动点，点F为CD边上一动点，且满足∠EOF=∠DAC，点E、F关于直线AC的对称点为G、H．分析 （1）根据菱形的性质得到AD=CD得到∠DAC=∠DCA，根据三角形的内角和和平角的定义得到∠FOC=∠AEO，于是得到结论；
（2）根据菱形的性质得到AO=3，BO=4，由勾股定理得到AD=CD=5，过O作OM⊥AD，ON⊥CD，根据三角形的面积公式得到OM=ON=$\frac{12}{5}$，根据相似三角形的性质得到CF=$\frac{9}{x}$，根据轴对称的性质得到S△AOG=S△AOE，S△COH=S△COF，于是得到结论；②当S=$\frac{72}{5}$时，求得x=3，得到AE=CF=3，DE=DF=2，根据相似三角形的判定和性质即刻得到结论．
解答 （1）证明：在菱形ABCD中，
∵AD=CD
∴∠DAC=∠DCA，
∵∠EOF=∠DAC，
∴∠AEO=180°-∠EAO-∠AOE，∠FOC=180°-∠AOE-∠EOF，
∴∠FOC=∠AEO，
∴△AOE∽△CFO；
（2）解：在菱形ABCD中，对角线AC、BD相交于点O，AC=6，BD=8，
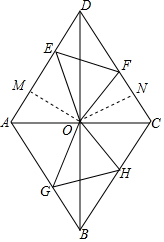
∴AO=3，BO=4，
∴AD=CD=5，
过O作OM⊥AD，ON⊥CD，
∴OM=ON=$\frac{12}{5}$，
∵△AOE∽△CFO，
∴$\frac{AE}{OC}=\frac{AO}{CF}$，
∴CF=$\frac{9}{x}$，
∵点E、F关于直线AC的对称点为G、H，
∴S△AOG=S△AOE，S△COH=S△COF，
∵①S△AOE=$\frac{6}{5}$x，S△COF=$\frac{54}{5x}$，
∴S=$\frac{12}{9}$（$\frac{9}{x}$+x）（$\frac{9}{5}≤x≤5$），
②当S=$\frac{72}{5}$时，x=3，
∴AE=CF=3，DE=DF=2，
∴$\frac{DE}{AD}=\frac{DF}{CD}$，∠ADC=∠EDF，
∴△DEF∽△ADC，
∴$\frac{EF}{6}=\frac{2}{5}$，
∴EF=$\frac{12}{5}$．
点评 本题考查了相似三角形的判定和性质，菱形的性质，轴对称的性质，求函数的解析式，熟练掌握相似三角形的性质是解题的关键．
每日10分钟口算心算速算天天练系列答案科目：初中数学 来源： 题型：解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com