
 将一副三角尺如图拼接:含30°角的三角尺(△ABC)的长直角边与含45°角的三角尺(△ACD)的斜边恰好重合.已知AB=4$\sqrt{3}$,点P在直线AC上.
将一副三角尺如图拼接:含30°角的三角尺(△ABC)的长直角边与含45°角的三角尺(△ACD)的斜边恰好重合.已知AB=4$\sqrt{3}$,点P在直线AC上.分析 (1)作DF⊥AC,在直角△BCP中,求得PC的长,而PF=CF-PC,则PF的长可以求得,然后在直角△DFP中利用勾股定理即可求解;
(2)作DF⊥AC,则P可以在F的左右两边,分两种情况进行讨论,与(1)的解法相同;
(3)分类讨论画出图形,不难判断Q的位置有3个,分别计算即可.
解答 解:(1)在Rt△ABC中,AB=4$\sqrt{3}$,∠BAC=30°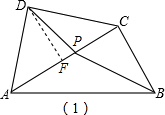
∴BC=2$\sqrt{3}$,AC=6.
如图(1),作DF⊥AC,
∵Rt△ACD中,AD=CD,
∴DF=AF=CF=3,
∵BP平分∠ABC,
∴∠PBC=30°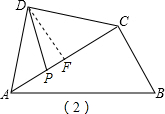 ,
,
∴CP=BC•tan30°=2,
∴PF=1,
∴DP=$\sqrt{D{F}^{2}+P{F}^{2}}$=$\sqrt{10}$.
(2)当P点位置如图(2)所示时,
根据(1)中结论,DF=3,∠ADF=45°
又∵PD=BC=2$\sqrt{3}$,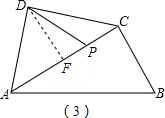
∴cos∠PDF=$\frac{DF}{PD}$=$\frac{\sqrt{3}}{2}$,
∴∠PDF=30°
∴∠PDA=∠ADF-∠PDF=15°
当P点位置如图(3)所示时,
同(2)可得∠PDF=30°.
∴∠PDA=∠ADF+∠PDF=75°.
(3)有3个,BQ=3或BQ=3+4$\sqrt{3}$,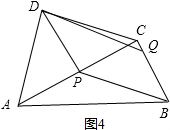
如图4、图5所示,DP⊥AC时,DP∥BQ,DP=BQ,则BQ=3,
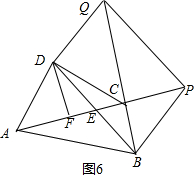
如图6所示,BD∥PQ,BD=PQ时,作DF⊥AC,
易证△DFE∽△BCE,△QCP∽△BCE,
∴$\frac{DE}{BE}=\frac{DF}{BC}=\frac{3}{2\sqrt{3}}=\frac{\sqrt{3}}{2}$,
∴$\frac{PQ}{BE}=\frac{BD}{BE}=\frac{2+\sqrt{3}}{2}=\frac{CQ}{BC}=\frac{CQ}{2\sqrt{3}}$,
∴CQ=3+2$\sqrt{3}$,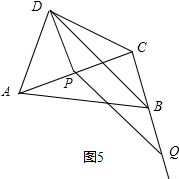
∴BQ=3+4$\sqrt{3}$,
故点Q有3个,BQ=3或BQ=3+4$\sqrt{3}$.
点评 本题考查了解直角三角形的应用,综合性较强,难度系数较大,关键是熟练掌握好边角之间的关系.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
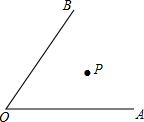 如图,某市的牛奶加工长P恰好在两条铁路OA、OB的夹角内部,为了提高牛奶的销量,经理决定在这两条铁路沿线上各建一个转运站M、N,加工厂的运货车每天从加工厂P向转运站M、N运送成品牛奶,问转运站M、N应建在何处,能够使运货车以最短的路程回到加工厂P?
如图,某市的牛奶加工长P恰好在两条铁路OA、OB的夹角内部,为了提高牛奶的销量,经理决定在这两条铁路沿线上各建一个转运站M、N,加工厂的运货车每天从加工厂P向转运站M、N运送成品牛奶,问转运站M、N应建在何处,能够使运货车以最短的路程回到加工厂P?查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 已知:如图,在直角坐标系中,有菱形OABC,A点的坐标为(10,0),对角线OB、AC相交于D点,双曲线y=$\frac{k}{x}$(x>0),经过D点,交BC的延长线于E点,且OB•AC=160,有下列四个结论:
已知:如图,在直角坐标系中,有菱形OABC,A点的坐标为(10,0),对角线OB、AC相交于D点,双曲线y=$\frac{k}{x}$(x>0),经过D点,交BC的延长线于E点,且OB•AC=160,有下列四个结论:查看答案和解析>>
科目:初中数学 来源: 题型:选择题

| A. | 只有(1)相似 | B. | 只有(2)相似 | C. | 都相似 | D. | 都不相似 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
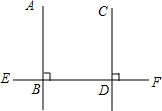 写出下列命题的已知、求证,并完成证明过程.
写出下列命题的已知、求证,并完成证明过程.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 观察探究,完成证明和填空.如图,在四边形ABCD中,点E、F、G、H分别是边AB、BC、CD、DA的中点,顺次连接E、F、G、H得到的四边形EFGH叫做中点四边形.
观察探究,完成证明和填空.如图,在四边形ABCD中,点E、F、G、H分别是边AB、BC、CD、DA的中点,顺次连接E、F、G、H得到的四边形EFGH叫做中点四边形.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com