
科目:初中数学 来源:2015年初中毕业升学考试(广东佛山卷)数学(解析版) 题型:解答题
(6分)(2015•佛山)若正比例函数y=k1x的图象与反比例函数y=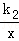 的图象有一个交点坐标是(﹣2,4)
的图象有一个交点坐标是(﹣2,4)
(1)求这两个函数的表达式;
(2)求这两个函数图象的另一个交点坐标.
查看答案和解析>>
科目:初中数学 来源:2015年初中毕业升学考试(福建泉州卷)数学(解析版) 题型:选择题
(3分)(2015•泉州)甲、乙、丙、丁四人参加训练,近期的10次百米测试平均成绩都是13.2秒,方差如表
选手 | 甲 | 乙 | 丙 | 丁 |
方差(秒2) | 0.020 | 0.019 | 0.021 | 0.022 |
则这四人中发挥最稳定的是( )
A.甲 B.乙 C.丙 D.丁
查看答案和解析>>
科目:初中数学 来源:2014-2015学年山东省泰安市中考模拟数学试卷(解析版) 题型:选择题
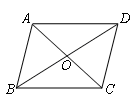
如图,四边形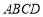 的对角线互相平分,要使它成为矩形,那么需要添加的条件是
的对角线互相平分,要使它成为矩形,那么需要添加的条件是
A.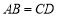 B.
B.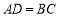
C.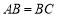 D.
D.
查看答案和解析>>
科目:初中数学 来源:2014-2015学年江苏省无锡市南长区九年级第一次模拟考试数学试卷(解析版) 题型:解答题
(本题满分10分)【问题情境】如图1,在△ABC中,AB=AC,点P为边BC上的任一点,过点P作PD⊥AB,PE⊥AC,垂足分别为D、E,过点C作CF⊥AB,垂足为F.求证:PD+PE=CF.
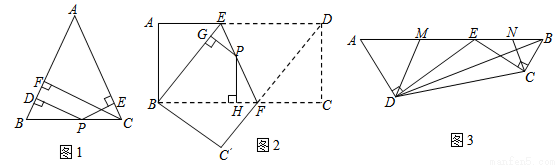
【结论运用】如图2,将矩形ABCD沿EF折叠,使点D落在点B上,点C落在点C′处,点P为折痕EF上的任一点,过点P作PG⊥BE、PH⊥BC,垂足分别为G、H,若AD=8,CF=3,求PG+PH的值;
【迁移拓展】图3是一个航模的截面示意图.在四边形ABCD中,E为AB边上的一点,ED⊥AD,EC⊥CB,垂足分别为D、C,且AD·CE=DE·BC,AB=8,AD=3,BD=7;M、N分别为AE、BE的中点,连接DM、CN,求△DEM与△CEN的周长之和.
查看答案和解析>>
科目:初中数学 来源:2014-2015学年湖北省襄阳市襄城区中考适应性考试数学试卷(解析版) 题型:选择题
二次函数y=a 的图象如图所示,
的图象如图所示,
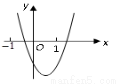
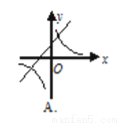
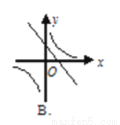
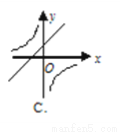
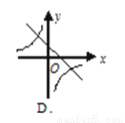
则一次函数y=bx+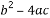 与反比例函数y=
与反比例函数y=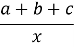 在同一坐标系内的图象大致为( )
在同一坐标系内的图象大致为( )
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com