
分析 将x=a,x=b分别代入f(x)=x3-3b2x+2c3,再化简,可得a=b=c,故可得三角形的形状.
解答 解:将x=a,x=b分别代入f(x)=x3-3bx2+2c2得:
a3-3ab2+2c3=0…①
b3-3b3+2c3=0…②
由②得2b3=2c3,
∴b=c,
∴a3-3ab2+2c3=a3-3ab2+2b3=a(a2-b2)-2b2(a-b)=(a-b)(a2-2b2+ab)=0,
∴a-b=0或a2-2b2+ab=0,
解a-b=0得a=b;
解关于a的方程a2+ba-2b2=0得a=b,
∴a=b=c,
∴三角形是等边三角形.
故答案为:等边.
点评 本题考查函数的零点,考查三角形形状的判断,考查学生分析解决问题的能力,正确理解函数的零点是关键.


科目:初中数学 来源: 题型:填空题
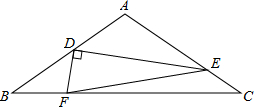 如图,在△ABC中,AB=AC,点D是AB中点,以D为直角顶点作∠EDF,分别交AC、BC于点E、F,连接EF,若tanB=$\frac{3}{4}$,BF=2,EF=3$\sqrt{5}$,则AE=5.
如图,在△ABC中,AB=AC,点D是AB中点,以D为直角顶点作∠EDF,分别交AC、BC于点E、F,连接EF,若tanB=$\frac{3}{4}$,BF=2,EF=3$\sqrt{5}$,则AE=5.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
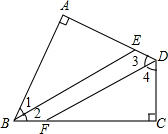 如图,四边形ABCD中,∠A=∠C=90°,BE平分∠ABC,DF平分∠ADC(提示:四边形内角和等于360°).
如图,四边形ABCD中,∠A=∠C=90°,BE平分∠ABC,DF平分∠ADC(提示:四边形内角和等于360°).查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
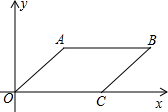 如图,平行四边形ABCO四个顶点的坐标分别为A($\sqrt{3}$,$\sqrt{3}$),B(3$\sqrt{3}$,$\sqrt{3}$),C(2$\sqrt{3}$,0),O(0,0),将这个平行四边形向左平移$\sqrt{3}$个单位长度,得到平行四边形A′B′C′O′,求平行四边形A′B′C′O′四个顶点的坐标.
如图,平行四边形ABCO四个顶点的坐标分别为A($\sqrt{3}$,$\sqrt{3}$),B(3$\sqrt{3}$,$\sqrt{3}$),C(2$\sqrt{3}$,0),O(0,0),将这个平行四边形向左平移$\sqrt{3}$个单位长度,得到平行四边形A′B′C′O′,求平行四边形A′B′C′O′四个顶点的坐标.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $\frac{{t}_{1}+{t}_{2}}{{t}_{2}-{t}_{1}}$ | B. | $\frac{{t}_{2}-{t}_{1}}{{t}_{2}+{t}_{1}}$ | C. | $\frac{{t}_{1}-{t}_{2}}{{t}_{2}+{t}_{1}}$ | D. | $\frac{{t}_{1}+{t}_{2}}{{t}_{1}-{t}_{2}}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $\sqrt{25}$=±5 | B. | |-3|=3 | C. | $\root{3}{9}$=3 | D. | $\sqrt{{(-4)}^{2}}$=-4 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com