
 ⊙O中,AB是直径,弦CD与AB交于E,AE=8,BE=2,∠AEC=30°,求CD的长.
⊙O中,AB是直径,弦CD与AB交于E,AE=8,BE=2,∠AEC=30°,求CD的长.| 1 |
| 2 |
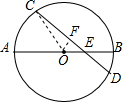 解:过点O作OF⊥CD于F,连接CO,
解:过点O作OF⊥CD于F,连接CO,| OC2-OF2 |
| ||
| 2 |
| 91 |


 科学实验活动册系列答案
科学实验活动册系列答案科目:初中数学 来源: 题型:
 有一个可以自由转动的转盘,被分成了4个相同的扇形,分别标有数1、2、3、4(如图所示),另有一个不透明的口袋装有分别标有数0、1、2的三个小球(除数字不同外,其余都相同).小亮转动一次转盘,停止后指针指向某一扇形,记下扇形所对应的数,
有一个可以自由转动的转盘,被分成了4个相同的扇形,分别标有数1、2、3、4(如图所示),另有一个不透明的口袋装有分别标有数0、1、2的三个小球(除数字不同外,其余都相同).小亮转动一次转盘,停止后指针指向某一扇形,记下扇形所对应的数,查看答案和解析>>
科目:初中数学 来源: 题型:
查看答案和解析>>
科目:初中数学 来源: 题型:
 芳芳用水管以均匀的速度向一个容器中注水,在注水过程中,水面的高度h与注水时间t之间的函数图象如图所示,最后芳芳将容器注满水,则这个容器的形状大致为( )
芳芳用水管以均匀的速度向一个容器中注水,在注水过程中,水面的高度h与注水时间t之间的函数图象如图所示,最后芳芳将容器注满水,则这个容器的形状大致为( )A、 |
B、 |
C、 |
D、 |
查看答案和解析>>
科目:初中数学 来源: 题型:
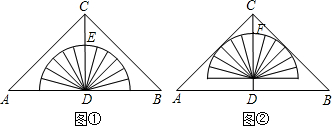
A、8+3
| ||
B、8+6
| ||
C、4+6
| ||
D、16+6
|
查看答案和解析>>
科目:初中数学 来源: 题型:
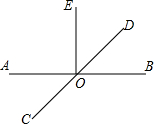 直线AB、CD相交于点O,∠AOC=45°,∠AOD=3∠DOE,图中的线是否存在互相垂直的关系?若存在,请写出互相垂直的线,并说明理由;若不存在,请直接说明理由.
直线AB、CD相交于点O,∠AOC=45°,∠AOD=3∠DOE,图中的线是否存在互相垂直的关系?若存在,请写出互相垂直的线,并说明理由;若不存在,请直接说明理由.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com