
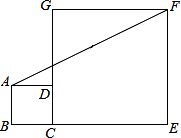
 如图,正方形ABCD和正方形CEFG中,点D在CG上,BC=1,CE=3,C到直线AF的距离是( )
如图,正方形ABCD和正方形CEFG中,点D在CG上,BC=1,CE=3,C到直线AF的距离是( )| A. | $\frac{3}{2}$$\sqrt{2}$ | B. | $\sqrt{5}$ | C. | $\frac{3}{5}$$\sqrt{5}$ | D. | 2 |
分析 作CH⊥AF,垂足为H.根据△ADK∽△FGK,求出KF的长,再根据△CHK∽△FGK,求出CH的长.
解答 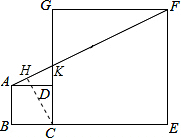 解:作CH⊥AF,垂足为H.
解:作CH⊥AF,垂足为H.
∵CD=BC=1,
∴GD=3-1=2,
∵△ADK∽△FGK,
∴$\frac{DK}{GK}$=$\frac{AD}{GF}$,
即$\frac{DK}{GK}$=$\frac{1}{3}$,
∴DK=2×$\frac{1}{4}$=$\frac{1}{2}$,GK=2×$\frac{3}{4}$=$\frac{3}{2}$,
∴KF=$\sqrt{(\frac{3}{2})^{2}+{3}^{2}}$=$\frac{3\sqrt{5}}{2}$,
∵△CHK∽△FGK,
∴$\frac{CH}{GF}$=$\frac{CK}{FK}$,
∴$\frac{CH}{3}$=$\frac{1+\frac{1}{2}}{\frac{3\sqrt{5}}{2}}$,
∴CH=$\frac{3\sqrt{5}}{5}$.
故选C.
点评 本题考查了勾股定理,利用勾股定理求出三角形的边长,再构造相似三角形是解题的关键.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,已知四边形ABCD是正方形,点E在DC边上,点F在CB边的延长线上,且DE=BF,连接AE,AF,EF.
如图,已知四边形ABCD是正方形,点E在DC边上,点F在CB边的延长线上,且DE=BF,连接AE,AF,EF.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
| 国外品牌 | 国内品牌 | |
| 进价(元/部) | 4400 | 2000 |
| 售价(元/部) | 5000 | 2500 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题

| A. | 10cm3以上,20cm3以下 | B. | 20cm3以上,30cm3以下 | ||
| C. | 30cm3以上,40cm3以下 | D. | 40cm3以上,50cm3以下 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com