
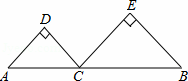
如图,线段AB的长为2,C为AB上一个动点,分别以AC、BC为斜边在AB的同侧作两个等腰直角三角形△ACD和△BCE,那么DE长的最小值是 .
考点:
二次函数的最值;等腰直角三角形。
专题:
计算题。
分析:
设AC=x,则BC=2-x,然后分别表示出DC、EC,继而在RT△DCE中,利用勾股定理求出DE的表达式,利用函数的知识进行解答即可.
解答:
解:如图,连接DE.
设AC=x,则BC=2-x,
∵△ACD和△BCE分别是等腰直角三角形,
∴∠DCA=45°,∠ECB=45°,DC=![]() ,CE=
,CE=![]() (2-x),
(2-x),
∴∠DCE=90°,
故DE2=DC2+CE2=![]() x2+
x2+![]() (2-x)2=x2-2x+2=(x-1)2+1,
(2-x)2=x2-2x+2=(x-1)2+1,
当x=1时,DE2取得最小值,DE也取得最小值,最小值为1.
故答案为:1.

点评:
此题考查了二次函数最值及等腰直角三角形,难度不大,关键是表示出DC、CE,得出DE的表达式,还要求我们掌握配方法求二次函数最值.


科目:初中数学 来源: 题型:
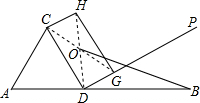 如图,线段AB的长为20
如图,线段AB的长为20| 2 |
| 2 |
| 2 |
查看答案和解析>>
科目:初中数学 来源: 题型:
 (2012•扬州)如图,线段AB的长为2,C为AB上一个动点,分别以AC、BC为斜边在AB的同侧作两个等腰直角三角形△ACD和△BCE,那么DE长的最小值是
(2012•扬州)如图,线段AB的长为2,C为AB上一个动点,分别以AC、BC为斜边在AB的同侧作两个等腰直角三角形△ACD和△BCE,那么DE长的最小值是查看答案和解析>>
科目:初中数学 来源: 题型:
 (2013•和平区二模)如图,线段AB的长为2,C为AB上一个动点,分别以AC、BC为斜边在AB的同侧作两个等腰直角三角形△ACD和△BCE,那么DE长的最小值是( )
(2013•和平区二模)如图,线段AB的长为2,C为AB上一个动点,分别以AC、BC为斜边在AB的同侧作两个等腰直角三角形△ACD和△BCE,那么DE长的最小值是( )查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com