解:(1)由图象得:
图中的线段AB表示的是甲的图象;
(2)设线段AB的函数关系式为y
1=k
1t,设线段CD的解析式为y
2=k
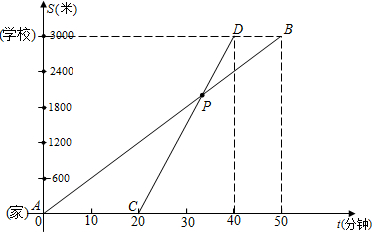
2t+b,根据题意,得
3000=50k
1或
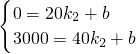
,
解得:k
1=60,

,
∴线段AB的解析式为:y
1=60t(0≤x≤50),
线段CD的解析式为:y
2=150t-3000(20≤x≤40),
(3)当y
1=y
2时,
150x-3000=60x,
解得:t=

,
∴y=2000,
∴P(

,2000).
(4)根据图象可以获得的信息有:
①甲的平均速度为3000÷50=60米/分,乙的平均速度为3000÷20=150米/分;
②甲、乙从家到学校的路程是3000米;
③乙比甲晚出发20分钟,乙比甲提前10分钟到达学校.
故答案为:AB;y
1=60t,y
2=150t-3000;(

,2000);①甲的平均速度为3000÷50=60米/分,乙的平均速度为3000÷20=150米/分;②甲、乙从家到学校的路程是3000米;③乙比甲晚出发20分钟,乙比甲提前10分钟到达学校.
分析:(1)由于甲是步行所以速度比较慢,在相同的路程下用时就较多,通过图象分析就可以得出线段OB表示甲的图象;
(2)运用待定系数法就可以直接求出线段AB和线段CD的函数关系式;
(3)根据(2)的解析式建立方程组求出其解就可以求出P点的坐标;
(4)通过图象观察可以求出甲的平均速度,可以求出乙的平均速度,甲乙两同学从家到学校的距离,乙比甲先到校的时间等信息.
点评:本题考查了一次函数的图象性质的运用,根据一次函数的图象信息获得相关的解题信息的运用,待定系数法求一次函数的解析式的运用,一次函数与二元一次方程组的关系的运用.解答本题的关键是读懂函数图象的意义.

 同校的甲、乙两同学的家刚好相邻,甲同学上学坚持步行,乙则骑自行车.下图是某天他俩上学时所走路程S(米)随时间t(分钟)变化的图象.根据图象回答问题:
同校的甲、乙两同学的家刚好相邻,甲同学上学坚持步行,乙则骑自行车.下图是某天他俩上学时所走路程S(米)随时间t(分钟)变化的图象.根据图象回答问题: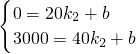 ,
, ,
, ,
, ,2000).
,2000). ,2000);①甲的平均速度为3000÷50=60米/分,乙的平均速度为3000÷20=150米/分;②甲、乙从家到学校的路程是3000米;③乙比甲晚出发20分钟,乙比甲提前10分钟到达学校.
,2000);①甲的平均速度为3000÷50=60米/分,乙的平均速度为3000÷20=150米/分;②甲、乙从家到学校的路程是3000米;③乙比甲晚出发20分钟,乙比甲提前10分钟到达学校.
