
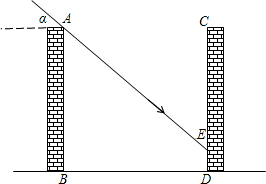
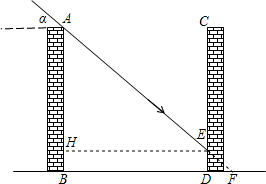
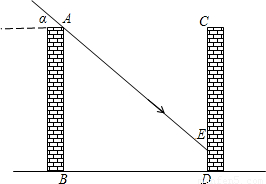
 解:(1)过点E作EH⊥AB,垂足为点H,
解:(1)过点E作EH⊥AB,垂足为点H,| AH |
| EH |
| BF |
| AB |


科目:初中数学 来源: 题型:
查看答案和解析>>
科目:初中数学 来源: 题型:
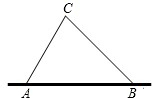 2009年4月23日是我国海军成立60周年纪念日,为此我国邀请了20多个国家的代表团和部分海军舰艇来青岛港参加庆祝活动,出于安全考虑,我军在青岛海域设置了供各国舰艇停放的安全区域,规定在海岸线AB以外12海里范围内为安全区域,任何其他船只不得进入,并通过海岸线设立的相距30海里的A、B两处观测站来实施监控.某天发现一艘可疑船只行驶至C处,观测员甲在A处测得C位于A的北偏东30°方向,同时观测员乙在B处测得C位于B的北偏西45°方向.试通过计算说明观测员是否需要向可疑船只发出警告,令其退回?(规定
2009年4月23日是我国海军成立60周年纪念日,为此我国邀请了20多个国家的代表团和部分海军舰艇来青岛港参加庆祝活动,出于安全考虑,我军在青岛海域设置了供各国舰艇停放的安全区域,规定在海岸线AB以外12海里范围内为安全区域,任何其他船只不得进入,并通过海岸线设立的相距30海里的A、B两处观测站来实施监控.某天发现一艘可疑船只行驶至C处,观测员甲在A处测得C位于A的北偏东30°方向,同时观测员乙在B处测得C位于B的北偏西45°方向.试通过计算说明观测员是否需要向可疑船只发出警告,令其退回?(规定| 2 |
| 3 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源:2010年上海市金山区中考数学一模试卷(解析版) 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com