练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    ）

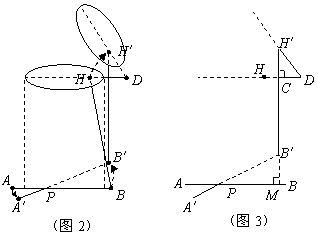
    如图1、图2，是一款家用的垃圾桶，踏板（与地面平行）或绕定点（固定在垃圾桶底部的某一位置）上下转动（转动过程中始终保持）．通过向下踩踏点到（与地面接触点）使点上升到点，与此同时传动杆运动到的位置，点绕固定点旋转（为旋转半径）至点，从而使桶盖打开一个张角．

    如图3，桶盖打开后，传动杆所在的直线分别与水平直线垂直，垂足为点，设=．测得．要使桶盖张开的角度不小于，那么踏板离地面的高度至少等于多少？（结果保留两位有效数字）

    （参考数据：）

    （图1）

    过点作垂足为点，

    在中，

    若不小于，

    则

    即

    踏板离地面的高度至少等于3.5cm．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    精英家教网已知：如图一次函数y=
    1
    2
    x+1的图象与x轴交于点A，与y轴交于点B；二次函数y=
    1
    2
    x2+bx+c的图象与一次函数y=
    1
    2
    x+1的图象交于B、C两点，与x轴交于D、E两点且D点坐标为（1，0）．
    （1）求二次函数的解析式；
    （2）求四边形BDEC的面积S；
    （3）在x轴上是否存在点P，使得△PBC是以P为直角顶点的直角三角形？若存在，求出所有的点P，若不存在，请说明理由．

    查看答案和解析>>

    科目：初中数学 来源：2009年甘肃省武威、金昌、定西、白银、酒泉、嘉峪关市中考数学试题及答案 题型：044

    如图(1)，抛物线y＝x2－2x＋k与x轴交于A、B两点，与y轴交于点C(0，－3)．[图(2)、图(3)为解答备用图]

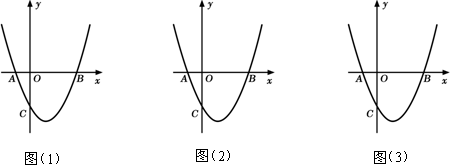
    (1)k＝________，点A的坐标为________，点B的坐标为________；

    (2)设抛物线y＝x2－2x＋k的顶点为M，求四边形ABMC的面积；

    (3)在x轴下方的抛物线上是否存在一点D，使四边形ABDC的面积最大？若存在，请求出点D的坐标；若不存在，请说明理由；

    (4)在抛物线y＝x2－2x＋k上求点Q，使△BCQ是以BC为直角边的直角三角形．

    查看答案和解析>>

    科目：初中数学 来源：2009年甘肃省武威、金昌、定西、白银、酒泉、嘉峪关市初中毕业、高中招生考试数学试题及答案 题型：059

    如图(1)，抛物线y＝x2－2x＋k与x轴交于A、B两点，与y轴交于点C(0，－3)．[图(2)、图(3)为解答备用图]

    (1)k＝________，点A的坐标为________，点B的坐标为________；

    (2)设抛物线y＝x2－2x＋k的顶点为M，求四边形ABMC的面积；

    (3)在x轴下方的抛物线上是否存在一点D，使四边形ABDC的面积最大？若存在，请求出点D的坐标；若不存在，请说明理由；

    (4)在抛物线y＝x2－2x＋k上求点Q，使△BCQ是以BC为直角边的直角三角形．

    查看答案和解析>>

    科目：初中数学 来源：2009年福建省宁德市中考网上阅卷模拟考试数学试卷（解析版） 题型：解答题

    如图1、图2，已知菱形ABCD，∠B=60°，M、N分别是BC、CD上一点，连接AM、AN．
    （1）如图1，当M、N分别是BC、CD中点时，求证：AM=AN；
    （2）如图2，当BM=CN时，求∠MAN的度数；
    （3）如图3，若将条件改为：已知菱形ABCD，∠B=α°（∠B是锐角，α是常数），M是线段BD上一点，N是直线CD上一点，设∠BAM=x°，∠DAN=y°．探究并说明当x、y满足怎样的数量关系时，线段AM=AN．

    查看答案和解析>>

    科目：初中数学 来源：2009年福建省宁德市初中学业质量检查数学试卷（解析版） 题型：解答题

    如图1、图2，已知菱形ABCD，∠B=60°，M、N分别是BC、CD上一点，连接AM、AN．
    （1）如图1，当M、N分别是BC、CD中点时，求证：AM=AN；
    （2）如图2，当BM=CN时，求∠MAN的度数；
    （3）如图3，若将条件改为：已知菱形ABCD，∠B=α°（∠B是锐角，α是常数），M是线段BD上一点，N是直线CD上一点，设∠BAM=x°，∠DAN=y°．探究并说明当x、y满足怎样的数量关系时，线段AM=AN．

    查看答案和解析>>

    同步练习册答案