
分析 (1)根据题意得出第8天剩余配料的重量=9天配料的重量-7天配料的重量,第9天剩余配料的重量=9天配料的重量-8天配料的重量,分别代入求出即可;7天的费用=70,8、9两天的费用=0.03×200×(1+2),相加求出即可;
(2)分两种情况列出总支出y(元)关于x的函数关系;
(3)由(2)可知:该厂平均每天的总支出有两种情况,设x天购买一次配料平均每天的总支出为W,则W=$\frac{370x+236}{x}$和W=$\frac{3{x}^{2}+321x+432}{x}$,求出它们的最值即可.
解答 解:(1)第8天剩余配料的重量为200×9-200×7=400(千克),
第9天剩余配料的重量为200×9-200×8=200(千克),
当9天购买一次配料,该厂的配料保管费用
P=70+0.03×(400+200)=88(元),
答:当9天购买一次配料时,该厂的配料保管费用P是88元.
(2)①当x≤7时,
y=360x+10x+236=370x+236;
②当x>7时,
y=360x+236+70+6[(x-7)+(x-6)+…+2+1]
=3x2+321x+432.
(3)设x天购买一次配料平均每天的总支出为W元,
①当≤7时,W=$\frac{270x+236}{x}$=270+$\frac{236}{x}$,
所以,x=7时,W有最小值,W最小值=270+$\frac{236}{7}$≈404;
②当>7时,W=$\frac{3{x}^{2}+321x+432}{x}$=3(x+$\frac{144}{x}$)+321,
当x=$\frac{144}{x}$时,W有最小值,
解得x=12,
所以,x=12时,W最小值=393;
综上,12天购买一次配料时,才能使该厂平均每天的总支出最少.
点评 本题考查了二次函数的最值,二次函数等知识点的理解和掌握,根据题意列出关系式是解题的关键.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,直线y=-x+3与x、y轴分别交于点A,B,与反比例函数的图象交于点P(2,1).
如图,直线y=-x+3与x、y轴分别交于点A,B,与反比例函数的图象交于点P(2,1).查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,河岸边有座塔AB,小敏在河对岸C处测得塔顶A的仰角为30°,向塔前进20米到达D处,又测得塔顶A的仰角为45°,请根据上述数据计算水塔的高.
如图,河岸边有座塔AB,小敏在河对岸C处测得塔顶A的仰角为30°,向塔前进20米到达D处,又测得塔顶A的仰角为45°,请根据上述数据计算水塔的高.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
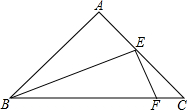 如图,在等腰三角形ABC中,AB=1,∠A=90°,点E为腰AC中点,点F在底边BC上,且FE⊥BE,求△CEF的面积是$\frac{1}{24}$.
如图,在等腰三角形ABC中,AB=1,∠A=90°,点E为腰AC中点,点F在底边BC上,且FE⊥BE,求△CEF的面积是$\frac{1}{24}$.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,点F、B、E、C在同一直线上,并且BF=CE,∠ABC=∠DEF,能否由上面的已知条件证明AC∥DF?如果能,请给出证明;如果不能,请从下列三个条件中选择一个合适的条件,添加到已知条件中,使AC∥DF,并给出证明.
如图,点F、B、E、C在同一直线上,并且BF=CE,∠ABC=∠DEF,能否由上面的已知条件证明AC∥DF?如果能,请给出证明;如果不能,请从下列三个条件中选择一个合适的条件,添加到已知条件中,使AC∥DF,并给出证明.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com