
分析 (1)先通过简单的计算,然后找出规律即可;
(2)利用发现的规律进行计算即可;
(3)依据上述规律计算出分子部分,然后再相加即可;
(2)先提出公因式2,然后再依据规律进行计算即可;
解答 解:(1)当n=2时,1+2=$\frac{2×(1+2)}{2}$=3;
当n=3时,1+2+3=$\frac{3×(1+3)}{2}$=6;
当n=4时,1+2+3+4=$\frac{4×(1+4)}{2}$=10;
…
1+2+3+…+n=$\frac{n(n+1)}{2}$;
故答案为:$\frac{n(n+1)}{2}$.
(2)1+2+3+4+…+100=$\frac{100×(1+100)}{2}$=5050;
(3)$\frac{1}{2}$+($\frac{1}{3}$+$\frac{2}{3}$)+($\frac{1}{4}$+$\frac{2}{4}$+$\frac{3}{4}$)+($\frac{1}{5}$+$\frac{2}{5}$+$\frac{3}{5}$+$\frac{4}{5}$)+…+($\frac{1}{50}$+$\frac{2}{50}$+$\frac{3}{50}$+…+$\frac{49}{50}$)
=$\frac{1}{2}$+1+$\frac{3}{2}$+2+$\frac{5}{2}$+…+$\frac{49}{2}$
=$\frac{49×(\frac{1}{2}+\frac{49}{2})}{2}$
=$\frac{1225}{2}$.
(4)2+4+6+…+2n=2×(1+2+3+4…+n)=2×$\frac{n(1+n)}{2}$=n(n+1).
点评 本题主要考查的是有理数的加法,找出其中的规律是解题的关键.


科目:初中数学 来源: 题型:填空题
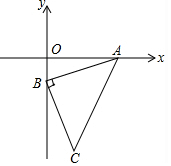 如图,在直角平面坐标系中,AB=BC,∠ABC=90°,A(3,0),B(0,-1),以AB为直角边在AB边的上方作等腰直角△ABE,则点E的坐标是(-1,2)或(2,3).
如图,在直角平面坐标系中,AB=BC,∠ABC=90°,A(3,0),B(0,-1),以AB为直角边在AB边的上方作等腰直角△ABE,则点E的坐标是(-1,2)或(2,3).查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
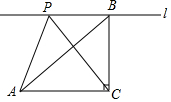 如图,在△ABC中,∠ACB=90°,AB=3cm,BC=2cm,直线l过点B,且l∥AC,点P是直线l上的一动点,连接AP,CP,点P在直线l上自左到右的运动过程中,△ACP的周长是如何变化的?如果不变,这个三角形的周长为多少?如果变化,这个三角形周长的最大值或最小值为多少?
如图,在△ABC中,∠ACB=90°,AB=3cm,BC=2cm,直线l过点B,且l∥AC,点P是直线l上的一动点,连接AP,CP,点P在直线l上自左到右的运动过程中,△ACP的周长是如何变化的?如果不变,这个三角形的周长为多少?如果变化,这个三角形周长的最大值或最小值为多少?查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com