
【题目】如图,△A1B1C1是边长为1的等边三角形,A2为等边△A1B1C1的中心,连接A2B1并延长到点B2 , 使A2B1=B1B2 , 以A2B2为边作等边△A2B2C2 , A3为等边
△A2B2C2的中心,连接A3B2并延长到点B3 , 使A3B2=B2B3 , 以A3B3为边作等边△A3B3C3 , 依次作下去得到等边△AnBnCn , 则等边△A5B5C5的边长为 . 
【答案】![]()
【解析】解:作A2D1⊥A1B1于D1 , A3D2⊥A2B2于D2 , 如图,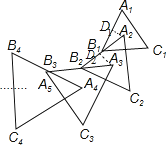
∵△A1B1C1是边长为1的等边三角形,A2为等边△A1B1C1的中心,
∴∠A2B1D1=30°,B1D1= ![]() A1B1=
A1B1= ![]() ,∴cos∠A2B1D1=cos30°=
,∴cos∠A2B1D1=cos30°= ![]() =
= ![]() ,∴A2B1=
,∴A2B1= ![]() ,
,
∵A2B1=B1B2 ,
∴A2B2= ![]() ,同理可得∠A3B2D2=30°,B2D2=
,同理可得∠A3B2D2=30°,B2D2= ![]() A2B2=
A2B2= ![]() ×
× ![]() =
= ![]() ,∴cos∠A3B2D2=cos30°=
,∴cos∠A3B2D2=cos30°= ![]() =
= ![]() ,∴A3B2=
,∴A3B2= ![]() ,
,
∵A3B2=B2B3 ,
∴A3B3= ![]() =(
=( ![]() )2=(
)2=( ![]() )2 , 同理可得A4B4=(
)2 , 同理可得A4B4=( ![]() )3 , A5B5=(
)3 , A5B5=( ![]() )4 . =
)4 . = ![]() 故答案为
故答案为 ![]() .
.
作A2D1⊥A1B1于D1 , A3D2⊥A2B2于D2 , 根据等边三角形的中心的性质得∠A2B1D1=30°,B1D1= ![]() A1B1=
A1B1= ![]() ,利用余弦的定义得cos∠A2B1D1=cos30°=
,利用余弦的定义得cos∠A2B1D1=cos30°= ![]() =
= ![]() ,可计算出A2B1=
,可计算出A2B1= ![]() ,由A2B1=B1B2得到A2B2=
,由A2B1=B1B2得到A2B2= ![]() ,用同样的方法可计算出A3B3=(
,用同样的方法可计算出A3B3=( ![]() )2 , 于是A4B4=(
)2 , 于是A4B4=( ![]() )3 , A5B5=(
)3 , A5B5=( ![]() )4 .
)4 .


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
【题目】如图,直线y=﹣x+b与双曲线 ![]() (x>0)交于A、B两点,与x轴、y轴分别交于E、F两点,连接OA、OB,若S△AOB=S△OBF+S△OAE , 则b= .
(x>0)交于A、B两点,与x轴、y轴分别交于E、F两点,连接OA、OB,若S△AOB=S△OBF+S△OAE , 则b= . 
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】计算
(1)(- 5)+ 6
(2)(+21)+(-31)
(3)(- 5.2 ) + ( - 1.2 )
(4)(﹣3)+7+(﹣6)+(﹣7)
(5)(- 20 ) +(-14)+(-28)+16
(6)5.6+(﹣0.9)+4.4+(﹣8.1)
(7)30 + 15+(-7)+(-15)
(8)![]() .
.
查看答案和解析>>
科目:初中数学 来源: 题型:
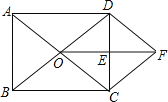
【题目】已知:如图,在矩形ABCD中,对角线AC、BD相交于点O,E是CD中点,连结OE.过点C作CF∥BD交线段OE的延长线于点F,连结DF.求证:
(1)△ODE≌△FCE;
(2)四边形ODFC是菱形.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在![]() ABCD中,AD=2AB,F是AD的中点,作
ABCD中,AD=2AB,F是AD的中点,作![]() ,垂足E在线段AB上,连接EF、CF,则下列结论中一定成立的是( )
,垂足E在线段AB上,连接EF、CF,则下列结论中一定成立的是( )

①![]() ②EF=CF
②EF=CF
③![]() ④
④![]()
A. ①②③ B. ①② C. ②③ ④ D. ①②④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】四边形ABCD各顶点的坐标分别为A(0,1)、B(5,1)、C(7,3)、D(2,5).

(1)在如图所示的平面直角坐标系画出该四边形;
(2)四边形ABCD的面积是________;
(3)四边形ABCD内(边界点除外)一共有_____个整点(即横坐标和纵坐标都是整数的点).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知OP平分∠AOB,∠AOB=60°,CP=2,CP∥OA,PD⊥OA于点D,PE⊥OB于点E.如果点M是OP的中点,则DM的长是( )

A. 2 B. ![]() C.
C. ![]() D. 2
D. 2![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校计划购买篮球、排球共20个,购买2个篮球,3个排球,共需花费190元;购买3个篮球的费用与购买5个排球的费用相同。
(1)篮球和排球的单价各是多少元?
(2)若购买篮球不少于8个,所需费用总额不超过800元.请你求出满足要求的所有购买方案,并直接写出其中最省钱的购买方案
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某企业生产部统计了15名工人某月的加工零件数:
每人加工零件数 | 540 | 450 | 300 | 240 | 210 | 120 |
人数 | 1 | 1 | 2 | 6 | 3 | 2 |
(1)求出这15人该月加工零件数的平均数并直接写出中位数和众数;
(2)若生产部领导把每位工人的月加工零件数定为260件,你认为合理否,为什么?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com