练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    如图所示表示的是一辆汽车在高速公路上行驶的情况，看图回答：

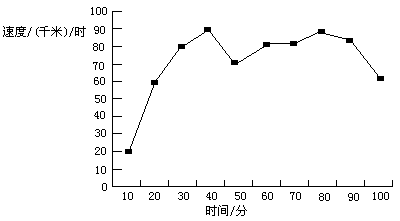
    (1)哪个是自变量？哪个是因变量？

    (2)什么时间速度最大，什么时间速度最小？各为多少？

    (3)什么时间内汽车在加速，什么时间内汽车的速度不变，什么时间内汽车在减速？

    答案：
    解析：

    　　(1)时间是自变量，速度是因变量．

    　　(2)行驶40分与80分时，速度最大为90千米／时；行驶10分时速度最小为20千米／时．

    　　(3)10～40分、50～80分汽车在加速，60～70分汽车的速度不变，40～50分、80～100分汽车在减速．


    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    如图①，一条笔直的公路上有A、B、C 三地，B、C 两地相距150 千米，甲、乙两辆汽车分别从B、C 两地同时出发，沿公路匀速相向而行，分别驶往C、B 两地．甲、乙两车到A 地的距离y1、y2 （千米）与行驶时间x（时）的关系如图②所示．根据图象进行以下探究：
    【图象理解】
    （1）填空：BA：AC=
     
    ，并在图①中标出A 地的大致位置．
    （2）图②中M 点的坐标为
     
    ，该点表示的实际意义是
     

    （3）在图②中补全甲车的函数图象，求甲车到A 的距离y1 与行驶时间x 的函数关系式．
    【问题解决】
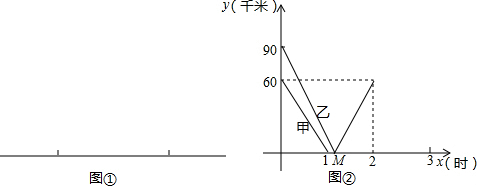
    （4）A地设有指挥中心，指挥中心及两车都配有对讲机，两部对讲机在15千米之内（含15 千米）时能够互相通话，求两车可以同时与指挥中心用对讲机通话的时间．精英家教网

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    如图，某隧道的截面是由一抛物线和一矩形构成，其行车道CD总宽度为8米，隧道为单行线2车道．
    （1）以矩形一边EF所在直线为x轴，经过隧道顶端最高点H且垂直于EF的直线为y轴，建立如图所示的平面直角坐标系，求出此抛物线的解析式；
    （2）在隧道拱的两侧距地面3米高处各安装一盏路灯，在（1）的平面直角坐标系中，用坐标表示其中一盏路灯的位置；
    （3）为了保证行车安全，要求行驶车辆顶部（设为平顶）与隧道拱在竖直方向上高度之差至少有0.5米．现有一辆汽车，装载货物后，其宽度为4米，车载货物的顶部与路面的距离为2.5米，该车能否通过这个隧道？请说明理由．
    精英家教网

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    据统计每年由于汽车超速行驶而造成的交通事故是造成人员死亡的主要原因之一．行驶中的汽车，在刹车后由于惯性的原因，还要继续向前滑行一段距离才能停住，这段距离称为“刹车距离”．为了测定某种型号汽车的刹车性能（车速不超过140千米/时），对这种汽车的刹车距离进行测试，测得的数据如下表：
    刹车时车速（千米/时） 0 5 10 15 20 25 30
    刹车距离（米） 0 0.1 0.3 0.6 1 1.5 2.1
    （1）在如图所示的直角坐标系中以车速为x轴，以刹车距离为y轴描出这些数据所表示的点，并用光滑的曲线连接这些点，得到某函数的大致图象．
    （2）观察图象估计函数的类型，并确定一个满足这些数据的函数解析式．
    （3）一辆该型号的汽车在国道上发生了交通事故，现场测得刹车距离为46.5米，请推测刹车时速度是多少？请问在事故发生时，汽车是否超速行驶？
    精英家教网

    查看答案和解析>>

    科目：初中数学 来源： 题型：

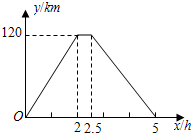    （1）一辆经营长途运输的货车在高速公路A处加满油后匀速行驶，下表记录的是货车一次加满油后油箱内余油y（升）与行驶时间x（时）之间的关系：
    行驶时间x（时） 0 1 2 2.5
    余油量y（升） 100 80 60 50
    ①请你认真分析上表中所给的数据，用你学过的一次函数、反比例函数和二次函数中的一种来表示y与x之间的变化规律，说明选择这种函数的理由，并求出它的函数表达式；（不要求写出自变量的取值范围）
    ②按照（1）中的变化规律，货车从A处出发行驶4.2小时到达B处，求此时油箱内余油多少升？
    （2）在一次救灾运输任务中，一辆汽车将一批救灾货物从甲地运往乙地，到达乙地卸货后返回．设汽车从甲地出发x（h）时，汽车与甲地的距离为y（km），y与x的函数关系如图所示．根据图象信息，解答下列问题：
    ①这辆汽车的往、返速度是否相同？请说明理由；
    ②求返程中y与x之间的函数表达式；
    ③求这辆汽车从甲地出发3h时与甲地的距离．

    查看答案和解析>>

    同步练习册答案