
 =3,求
=3,求 的值.
的值.
 的值是______.
的值是______.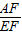 =m(m>0),则
=m(m>0),则 的值是______(用含有m的代数式表示),试写出解答过程.
的值是______(用含有m的代数式表示),试写出解答过程. =a,
=a, =b,(a>0,b>0)
=b,(a>0,b>0)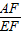 的值是______(用含a、b的代数式表示).
的值是______(用含a、b的代数式表示).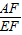 =3是一个确定的数值.如答图1,过E点作平行线,构造相似三角形,利用相似三角形和中位线的性质,分别将各相关线段均统一用EH来表示,最后求得比值;
=3是一个确定的数值.如答图1,过E点作平行线,构造相似三角形,利用相似三角形和中位线的性质,分别将各相关线段均统一用EH来表示,最后求得比值;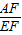 =m不再是一个确定的数值,但(1)问中的解题方法依然适用,如答图2所示.
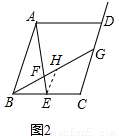
=m不再是一个确定的数值,但(1)问中的解题方法依然适用,如答图2所示.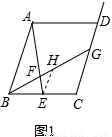 依题意,过点E作EH∥AB交BG于点H,如右图1所示.
依题意,过点E作EH∥AB交BG于点H,如右图1所示.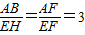 ,∴AB=3EH.
,∴AB=3EH. =
=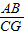 =
=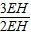 =
= .
. .
.
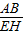 =
=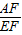 =m,∴AB=mEH.
=m,∴AB=mEH.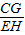 =
=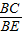 =2,∴CG=2EH.…6分
=2,∴CG=2EH.…6分 =
=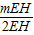 =
=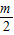 .
.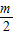 .
.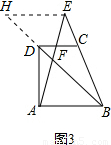 如右图3所示,过点E作EH∥AB交BD的延长线于点H,则有EH∥AB∥CD.
如右图3所示,过点E作EH∥AB交BD的延长线于点H,则有EH∥AB∥CD.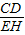 =
= =b,∴CD=bEH.
=b,∴CD=bEH.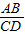 =a,∴AB=aCD=abEH.
=a,∴AB=aCD=abEH. =
=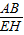 =
=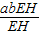 =ab,
=ab,

科目:初中数学 来源: 题型:
| AF |
| EF |
| CD |
| CG |

| CD |
| CG |
| 3 |
| 2 |
| 3 |
| 2 |
| AF |
| EF |
| CD |
| CG |
| m |
| 2 |
| m |
| 2 |
| AB |
| CD |
| BC |
| BE |
| AF |
| EF |
查看答案和解析>>
科目:初中数学 来源: 题型:
| AF |
| EF |
| CD |
| CG |

| AB |
| EH |
| CG |
| EH |
| CD |
| CG |
| 3 |
| 2 |
| 3 |
| 2 |
| AF |
| EF |
| CD |
| CG |
| m |
| 2 |
| m |
| 2 |
| AB |
| CD |
| BC |
| BE |
| AF |
| EF |
查看答案和解析>>
科目:初中数学 来源:2012年初中毕业升学考试(河南洛阳卷)数学(带解析) 题型:解答题
类比、转化、从特殊到一般等思想方法,在数学学习和研究中经常用到,如下是一个案例,请补充完整.
原题:如图1,在 中,点E是BC边上的中点,点F是线段AE上一点,BF的延长线交射线CD于点G,若
中,点E是BC边上的中点,点F是线段AE上一点,BF的延长线交射线CD于点G,若 ,求
,求 的值。
的值。
(1)尝试探究
在图1中,过点E作 交BG于点H,则AB和EH的数量关系是 ,CG和EH的数量关系是 ,
交BG于点H,则AB和EH的数量关系是 ,CG和EH的数量关系是 , 的值是
的值是
(2)类比延伸
如图2,在原题的条件下,若 则
则 的值是 (用含
的值是 (用含 的代数式表示),试写出解答过程。
的代数式表示),试写出解答过程。
(3)拓展迁移
如图3,梯形ABCD中,DC∥AB,点E是BC延长线上一点,AE和BD相交于点F,若 ,则
,则 的值是 (用含
的值是 (用含 的代数式表示).
的代数式表示).
查看答案和解析>>
科目:初中数学 来源:2013届江苏省阜宁县九年级第一次调研数学试卷(带解析) 题型:解答题
在数学学习和研究中经常需要总结运用数学思想方法。如类比、转化、从特殊到一般等思想方法,如下是一个案例,请补充完整。
题目:如图1,在平行四边形ABCD中,点E是BC的中点,点F在线段AE上,BF的延长线交射线CD于点G,若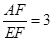 ,求
,求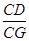 的值。
的值。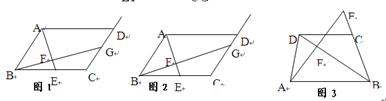
(1)尝试探究
在图1中,过点E作EH∥AB交BG于点H,则易求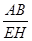 的值是 ,
的值是 ,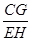 的值是
的值是
,从而确定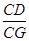 的值是 。
的值是 。
(2)类比延伸
如图2,在原题的条件下,若 ,则
,则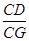 的值是 。(用含m的代数式表示),写出解答过程。
的值是 。(用含m的代数式表示),写出解答过程。
(3)拓展迁移
如图3,在梯形ABCD中,DC∥AB,点E是BC延长线上的一点,AE和BD相交于F,若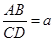 ,
,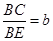 (a>0,b>0),则
(a>0,b>0),则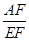 的值是 。(用含a、b的代数式表示)写出解答过程。
的值是 。(用含a、b的代数式表示)写出解答过程。
查看答案和解析>>
科目:初中数学 来源:2012-2013学年江苏省阜宁县九年级第一次调研数学试卷(解析版) 题型:解答题
在数学学习和研究中经常需要总结运用数学思想方法。如类比、转化、从特殊到一般等思想方法,如下是一个案例,请补充完整。
题目:如图1,在平行四边形ABCD中,点E是BC的中点,点F在线段AE上,BF的延长线交射线CD于点G,若 ,求
,求 的值。
的值。

(1)尝试探究
在图1中,过点E作EH∥AB交BG于点H,则易求 的值是 ,
的值是 , 的值是
的值是
,从而确定 的值是 。
的值是 。
(2)类比延伸
如图2,在原题的条件下,若 ,则
,则 的值是 。(用含m的代数式表示),写出解答过程。
的值是 。(用含m的代数式表示),写出解答过程。
(3)拓展迁移
如图3,在梯形ABCD中,DC∥AB,点E是BC延长线上的一点,AE和BD相交于F,若 ,
, (a>0,b>0),则
(a>0,b>0),则 的值是 。(用含a、b的代数式表示)写出解答过程。
的值是 。(用含a、b的代数式表示)写出解答过程。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com