Question

周长相等的正方形和正六边形的面积分别为S₄和S₆，则S₄和S₆的大小关系为______．

Answer 1

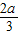
【答案】分析：根据题意画出图形，设正方形ABCD的边长为a，则正六边形EFGHIK的边长为，再分别用a表示出各图形的面积，再进行比较即可．
解答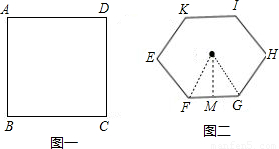：解：如图所示，
设正方形ABCD的边长为a，
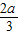
则正六边形EFGHIK的边长为，S_□ABCD=a²；
如图（二）所示，
∵六边形EFGHIK是正六边形，
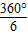
∴∠GOF==60°，
∵OF=OG，
∴FM=GF=×=，
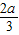
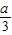
∴OM===，
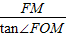
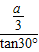
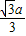
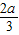
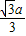
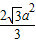
∴S正六边形EFGHIK=6×GF×OM=3××=＞a²，
故答案为：S₄＜S₆．
点评：本题考查的是正多边形的面积，熟知正方形及正六边形的面积是解答此题的关键．