
【题目】如图,下列各语句中,错误的语句是( ) 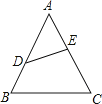
A.∠ADE与∠B是同位角
B.∠BDE与∠C是同旁内角
C.∠BDE与∠AED是内错角
D.∠BDE与∠DEC是同旁内角
【答案】B
【解析】A、由同位角的概念可知,∠ADE与∠B是同位角,不符合题意;B、由同位角同旁内角的概念可知,∠BDE与∠C不是同旁内角,符合题意;C、由内错角的概念可知,∠BDE与∠AED是内错角,不符合题意;D、由同旁内角的概念可知,∠BDE与∠DEC是同旁内角,不符合题意. 故选B.
根据同位角:两条直线被第三条直线所截形成的角中,若两个角都在两直线的同侧,并且在第三条直线(截线)的同旁,则这样一对角叫做同位角.内错角:两条直线被第三条直线所截形成的角中,若两个角都在两直线的之间,并且在第三条直线(截线)的两旁,则这样一对角叫做内错角.同旁内角:两条直线被第三条直线所截形成的角中,若两个角都在两直线的之间,并且在第三条直线(截线)的同旁,则这样一对角叫做同旁内角作答.


 核心素养学练评系列答案
核心素养学练评系列答案 单元期中期末卷系列答案
单元期中期末卷系列答案科目:初中数学 来源: 题型:
【题目】已知AB∥CD,以点B为圆心,小于DB长为半径作圆弧,分别交BA、BD于点E、F,再分别以点E、F为圆心,大于 ![]() EF长为半径作圆弧,两弧交于点G,作射线BG交CD于点H.若∠D=116°,则∠DHB的大小为度.
EF长为半径作圆弧,两弧交于点G,作射线BG交CD于点H.若∠D=116°,则∠DHB的大小为度.
查看答案和解析>>
科目:初中数学 来源: 题型:
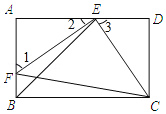
【题目】如图,E,F分别是矩形ABCD的边AD,AB上的点,若EF=EC,且EF⊥EC.
(1)求证:△AEF≌△DCE;
(2)若CD=1,求BE的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我国古代数学的许多发现都曾位居世界前列,其中“杨辉三角”(如图所示)就是一例. 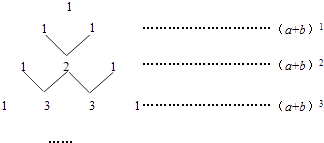
这个三角形的构造法则为:两腰上的数都是1,其余每个数均为其上方左右两数之和.事实上,这个三角形给出了(a+b)n(n为正整数)的展开式(按a的次数由大到小的顺序排列)的系数规律.例如,在三角形中第三行的三个数1,2,1,恰好对应(a+b)2=a2+ab+b2展开式中各项的系数;第四行的四个数1,3,3,1,恰好对应着(a+b)3=a3+3a2b+3ab2+b3展开式中各项的系数等等.根据上面的规律,(a+b)4的展开式中各项系数最大的数为( )
A.4
B.5
C.6
D.7
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,在平面直角坐标系中. 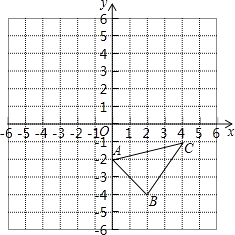
(1)作出△ABC 关于y轴对称的△A1B1C1 , 并写出△A1B1C1三个顶点的坐标:A1(),B1(),C1();
(2)直接写出△ABC的面积为;
(3)在x轴上画点P,使PA+PC最小.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】当a < 0 时,方程ax2+bx+c=0无实数根,则二次函数y=ax2+bx+c的图像一定在 ( )
A、x轴上方 B、x轴下方 C、y轴右侧 D、y轴左侧
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】化简求值。
(1)已知x+y=15,x2+y2=113,求x2﹣xy+y2的值.
(2)先化简,再求值: ![]() ÷
÷ ![]() +1,在0,1,2,三个数中选一个合适的,代入求值.
+1,在0,1,2,三个数中选一个合适的,代入求值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com