
如图,直线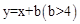 与x轴、y轴分别相交于点A、B,与正比例函数
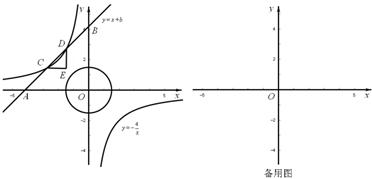
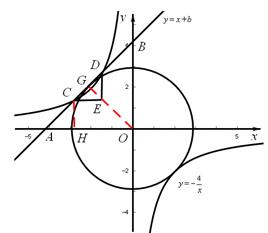
与x轴、y轴分别相交于点A、B,与正比例函数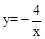 的图象相交于点C、D(点C在点D的左侧),⊙O是以CD长为半径的圆。CE∥x轴,DE∥y轴,CE、DE相交于点E。
的图象相交于点C、D(点C在点D的左侧),⊙O是以CD长为半径的圆。CE∥x轴,DE∥y轴,CE、DE相交于点E。
(1)△CDE是 ▲ 三角形;点C的坐标为 ▲ ,点D的坐标为 ▲ (用含有b的代数式表示);
(2)b为何值时,点E在⊙O上?
(3)随着b取值逐渐增大,直线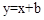 与⊙O有哪些位置关系?求出相应b的取值范围。
与⊙O有哪些位置关系?求出相应b的取值范围。
(1)等腰直角; ;
;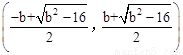 。(2)
。(2)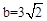 时,点E在⊙O上(3)见解析
时,点E在⊙O上(3)见解析
【解析】解:(1)等腰直角; ;
;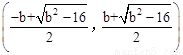 。
。
(2)当点E在⊙O上时,如图,连接OE。则OE=CD。

∵直线 与x轴、y轴相交于点A(-b,0),B(0,b),CE∥x轴,DE∥y轴,
与x轴、y轴相交于点A(-b,0),B(0,b),CE∥x轴,DE∥y轴,
∴△DCE、△BDO是等腰直角三角形。
∵整个图形是轴对称图形,
∴OE平分∠AOB,∠AOE=∠BOE=450。
∵CE∥x轴,DE∥y轴,
∴四边形CAOE、OEDB是等腰梯形。
∴OE=AC=BD。
∵OE=CD,∴OE=AC=BD=CD。
过点C作CF⊥x轴,垂足为点F。
则△AFC∽△AOB。∴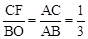 。∴
。∴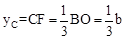 。
。
∴ ,解得
,解得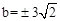 。
。
∵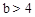 ,∴
,∴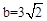 。
。
∴当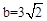 时,点E在⊙O上。
时,点E在⊙O上。
(3)当⊙O与直线 相切于点G时,
相切于点G时,
如图 ,连接OG。
∵整个图形是轴对称图形,
∴点O、E、G在对称轴上。
∴GC=GD= CD=
CD= OG=
OG= AG。∴AC=CG=GD=DB。∴AC=
AG。∴AC=CG=GD=DB。∴AC= AB。
AB。
过点C作CH⊥x轴,垂足为点H。 则△AHC∽△AOB。
∴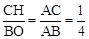 。∴
。∴ 。
。
∴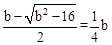 ,解得
,解得 。
。
∵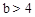 ,∴
,∴ 。
。
∴当 时,直线
时,直线 与⊙O相切;
与⊙O相切;
当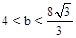 时,直线
时,直线 与⊙O相离;
与⊙O相离;
当 时,直线
时,直线 与⊙O相交。
与⊙O相交。
(1)∵直线 与x轴、y轴相交于点A(-b,0),B(0,b),CE∥x轴,DE∥y轴,
与x轴、y轴相交于点A(-b,0),B(0,b),CE∥x轴,DE∥y轴,
∴△DCE是等腰直角三角形。
解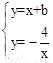 得,
得, 或
或 。
。
∵点C在点D的左侧,∴点C的坐标为 ,点D的坐标为
,点D的坐标为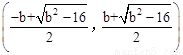 。
。
(2)连接OE,过点C作CH⊥x轴于点H。由整个图形是轴对称图形,可求得OE=AC=BD=CD。由△AFC∽△AOB可求得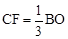 ,代入CF、BO关于b的关系式求解即得所求。
,代入CF、BO关于b的关系式求解即得所求。
(3)讨论直线 与⊙O相切时,b的取值即可得到直线
与⊙O相切时,b的取值即可得到直线 与⊙O的位置关系。
与⊙O的位置关系。
当⊙O与直线 相切于点G时,连接OG,过点C作CH⊥x轴于点H。由整个图形是轴对称图形,可求得AC=CG=GD=DB,即AC=
相切于点G时,连接OG,过点C作CH⊥x轴于点H。由整个图形是轴对称图形,可求得AC=CG=GD=DB,即AC= AB。由△AHC∽△AOB可求得
AB。由△AHC∽△AOB可求得 ,代入CH、BO关于b的关系式求解即得⊙O与直线
,代入CH、BO关于b的关系式求解即得⊙O与直线 相切时相应b的值。从而得到直线
相切时相应b的值。从而得到直线 与⊙O相离和相交时相应b的取值范围。
与⊙O相离和相交时相应b的取值范围。


 英才点津系列答案
英才点津系列答案 红果子三级测试卷系列答案
红果子三级测试卷系列答案科目:初中数学 来源: 题型:
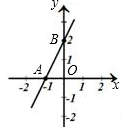 如图,直线与x轴、y轴分别交于A、B两点.
如图,直线与x轴、y轴分别交于A、B两点.查看答案和解析>>
科目:初中数学 来源: 题型:
| 1 |
| 2x |
| 1 |
| 2x |
查看答案和解析>>
科目:初中数学 来源: 题型:
 如图,直线与x轴、y轴分别交于A、B两点.
如图,直线与x轴、y轴分别交于A、B两点.查看答案和解析>>
科目:初中数学 来源:2011届宁夏银川市初三上学期期末数学卷 题型:解答题
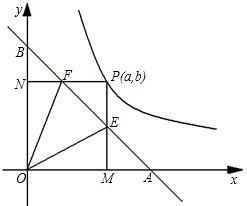
如图①,直线 与x轴、y轴分别交于B、C两点,点A在x轴负半轴上,且
与x轴、y轴分别交于B、C两点,点A在x轴负半轴上,且 ,抛物线经过A、B、C三点,D为线段AB中点,点P(m,n)是该抛物线上的一个动点(其中m>0,n<0),连接DP交BC于点E.
,抛物线经过A、B、C三点,D为线段AB中点,点P(m,n)是该抛物线上的一个动点(其中m>0,n<0),连接DP交BC于点E.
(1)写出A、B、C三点的坐标,并求抛物线的解析式;(5分)
(2) 当△BDE是等腰三角形时,直接写出此时点E的坐标;(3分)
(3)连结PC、PB,△PBC是否有最大面积?若有,求出△PBC的最大面积和此时P点的坐标;若没有,请说明理由。(3分)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com