
 如图所示,一条小河的两岸l1∥l2,和两岸各有一座建筑A和B,为测得A,B间的距离,小明从点B出发,沿垂直河岸l2的方向上选一点C,然后沿垂直于BC的直线行进了24米到达D,测得∠CDA=90°,取CD的中点E,测得∠BEC=56°,∠AED=67°,求A,B间的距离.(参考数据:sin56°≈
如图所示,一条小河的两岸l1∥l2,和两岸各有一座建筑A和B,为测得A,B间的距离,小明从点B出发,沿垂直河岸l2的方向上选一点C,然后沿垂直于BC的直线行进了24米到达D,测得∠CDA=90°,取CD的中点E,测得∠BEC=56°,∠AED=67°,求A,B间的距离.(参考数据:sin56°≈ tan56°≈
tan56°≈ sin67°≈
sin67°≈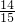 tan67°≈
tan67°≈ 262=676272=729)
262=676272=729)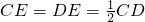 =
= ×24=12(米),
×24=12(米),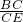 ,
, =18,
=18, ,
, =28,
=28,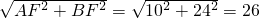 (米).
(米).

科目:初中数学 来源: 题型:
 19、如图所示,A、B两村在一条小河的的同一侧,现要在河边建一水厂P向两村供水,若要使自来水厂P到两村的距离和最短,厂址应选在哪个位置最合适?(并保留作图痕迹)
19、如图所示,A、B两村在一条小河的的同一侧,现要在河边建一水厂P向两村供水,若要使自来水厂P到两村的距离和最短,厂址应选在哪个位置最合适?(并保留作图痕迹)查看答案和解析>>
科目:初中数学 来源: 题型:
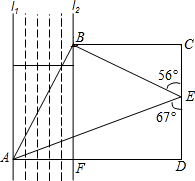 (2012•郑州模拟)如图所示,一条小河的两岸l1∥l2,和两岸各有一座建筑A和B,为测得A,B间的距离,小明从点B出发,沿垂直河岸l2的方向上选一点C,然后沿垂直于BC的直线行进了24米到达D,测得∠CDA=90°,取CD的中点E,测得∠BEC=56°,∠AED=67°,求A,B间的距离.(参考数据:sin56°≈
(2012•郑州模拟)如图所示,一条小河的两岸l1∥l2,和两岸各有一座建筑A和B,为测得A,B间的距离,小明从点B出发,沿垂直河岸l2的方向上选一点C,然后沿垂直于BC的直线行进了24米到达D,测得∠CDA=90°,取CD的中点E,测得∠BEC=56°,∠AED=67°,求A,B间的距离.(参考数据:sin56°≈| 4 |
| 5 |
| 3 |
| 2 |
| 14 |
| 15 |
| 7 |
| 3 |
查看答案和解析>>
科目:初中数学 来源:2012年河南省郑州市中考第一次质量预测数学试卷(解析版) 题型:解答题
 tan56°≈
tan56°≈ sin67°≈
sin67°≈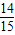 tan67°≈
tan67°≈ 262=676272=729)
262=676272=729)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com