
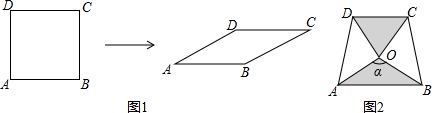
| α | 30° | 45° | 60° | 90° | 120° | 135° | 150° |
| S | $\frac{1}{2}$ | 1 | $\frac{{\sqrt{2}}}{2}$ |
分析 (1)过D作DE⊥AB于点E,当α=45°时,可求得DE,从而可求得菱形的面积S,同理可求当α=60°时S的值,当α=120°时,过D作DF⊥AB交BA的延长线于点F,则可求得DF,可求得S的值,同理当α=135°时S的值;
(2)根据表中所计算出的S的值,可得出答案;
(3)将△ABO沿AB翻折得到菱形AEBO,将△CDO沿CD翻折得到菱形OCFD.利用(2)中的结论,可求得△AOB和△COD的面积,从而可求得结论.
解答 解:
(1)当α=45°时,如图1,过D作DE⊥AB于点E,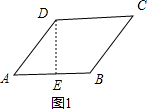
则DE=$\frac{\sqrt{2}}{2}$AD=$\frac{\sqrt{2}}{2}$,
∴S=AB•DE=$\frac{\sqrt{2}}{2}$,
同理当α=60°时S=$\frac{\sqrt{3}}{2}$,
当α=120°时,如图2,过D作DF⊥AB,交BA的延长线于点F,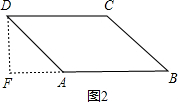
则∠DAE=60°,
∴DF=$\frac{\sqrt{3}}{2}$AD=$\frac{\sqrt{3}}{2}$,
∴S=AB•DF=$\frac{\sqrt{3}}{2}$,
同理当α=150°时,可求得S=$\frac{1}{2}$,
故表中依次填写:$\frac{{\sqrt{2}}}{2}$;$\frac{{\sqrt{3}}}{2}$;$\frac{{\sqrt{3}}}{2}$;$\frac{1}{2}$;
(2)由(1)可知S(60°)=S(120°),
S(150°)=S(30°),
∴S(180°-α)=S(α)
故答案为:120;30;α;
(3)两个带阴影的三角形面积相等.
证明:如图3将△ABO沿AB翻折得到菱形AMBO,将△CDO沿CD翻折得到菱形OCND.
∵∠AOD=∠COB=90°,
∴∠COD+∠AOB=180°,
∴S△AOB=$\frac{1}{2}$S菱形AMBO=$\frac{1}{2}$S(α)
S△CDO=$\frac{1}{2}$S菱形OCND=$\frac{1}{2}$S(180°-α)
由(2)中结论S(α)=S(180°-α)
∴S△AOB=S△CDO.
点评 本题为四边形的综合应用,涉及知识点有菱形的性质和面积、解直角三角形及转化思想等.在(1)中求得菱形的高是解题的关键,在(2)中利用好(1)中的结论即可,在(3)中把三角形的面积转化成菱形的面积是解题的关键.本题考查知识点较基础,难度不大.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com