
 ,抛物线
,抛物线 过A、B两点.
过A、B两点.
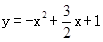 ,直线AB的解析式为:
,直线AB的解析式为: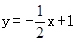 ;
;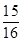 ;(3)当
;(3)当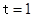 时,
时,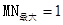
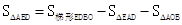 ,即可求出.
,即可求出. :
: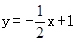 上,N在抛物线
上,N在抛物线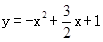 上,可以用t表示出MN的长度,即可找出t为何值时,MN的值最大.
上,可以用t表示出MN的长度,即可找出t为何值时,MN的值最大.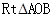 中,
中,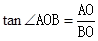
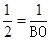
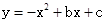 过A(0,1),B(2,0)
过A(0,1),B(2,0)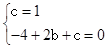
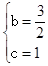
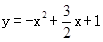
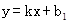 ,将A(0,1),B(2,0)代入
,将A(0,1),B(2,0)代入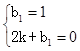 解得:
解得: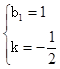
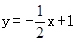
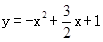
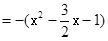
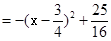

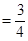 ,EO=
,EO=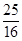
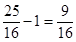
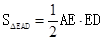

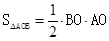
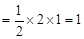
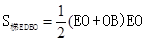
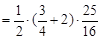
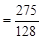


 :
: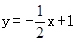 上
上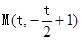
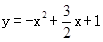 上
上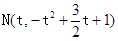
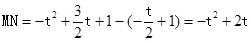
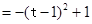 ,其中
,其中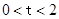 .
.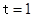 时,
时,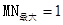


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源:不详 题型:解答题
| 销售单价(元) | 50 | 53 | 56 | 59 | 62 | 65 |
| 月销售量(千克) | 420 | 360 | 300 | 240 | 180 | 120 |
查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题
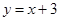 与x轴、y轴分别交于点A、C,经过A、C两点的抛物线
与x轴、y轴分别交于点A、C,经过A、C两点的抛物线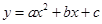 与x轴的负半轴上另一交点为B,且tan∠CBO=3.
与x轴的负半轴上另一交点为B,且tan∠CBO=3.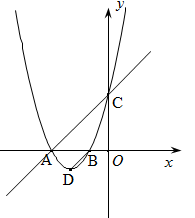
查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题
 .
. 与
与 在此二次函数的图象上,则
在此二次函数的图象上,则
 (填 “>”、“=”或“<”);
(填 “>”、“=”或“<”); ,正方形ABCD的顶点C、D在x轴上, A、B恰好在二次函数的图象上,求图中阴影部分的面积之和.
,正方形ABCD的顶点C、D在x轴上, A、B恰好在二次函数的图象上,求图中阴影部分的面积之和.
查看答案和解析>>
科目:初中数学 来源:不详 题型:单选题
| A.y=(x+1)2+4 | B.y=(x-1)2+4 |
| C.y=(x+1)2+2 | D.y=(x-1)2+2 |
查看答案和解析>>
科目:初中数学 来源:不详 题型:单选题

| A.1个 | B.2个 | C.3个 | D.4个 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com