
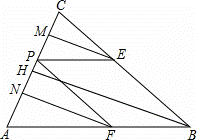
��ͼ����ABC�У�AB=BC��AC=8��tanA=k��PΪAC����һ���㣬��PC=x����PE��AB��BC��E��PF��BC��AB��F��
��1��֤������PCE�ǵ��������Σ�
��2��EM��FN��BH�ֱ��ǡ�PEC����AFP����ABC�ĸߣ��ú�x��k�Ĵ���ʽ��ʾEM��FN����̽��EM��FN��BH֮���������ϵ��
��3����k=4ʱ�����ı���PEBF�����S��x�ĺ�����ϵʽ��xΪ��ֵʱ��S�����ֵ�������S�����ֵ��
��1��֤������AB=BC��
���A=��C��
��PE��AB��
���CPE=��A��
���CPE=��C��
���PCE�ǵ��������Σ�
��2���⣺�ߡ�PCE�ǵ��������Σ�EM��CP��
��CM=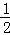 CP=
CP=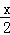 ��tanC=tanA=k��
��tanC=tanA=k��
��EM=CM•tanC=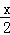 •k=
•k=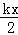 ��
��
ͬ����FN=AN•tanA= •k=4k��
•k=4k��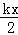 ��
��
����BH=AH•tanA=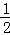 ��8•k=4k��
��8•k=4k��
��EM+FN=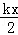 +4k��
+4k��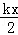 =4k��
=4k��
��EM+FN=BH��
��3���⣺��k=4ʱ��EM=2x��FN=16��2x��BH=16��
���ԣ�S��PCE=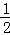 x•2x=x2��S��APF=
x•2x=x2��S��APF=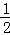 ��8��x��•��16��2x��=��8��x��2��S��ABC=
��8��x��•��16��2x��=��8��x��2��S��ABC=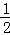 ��8��16=64��
��8��16=64��
S=S��ABC��S��PCE��S��APF��xK b1. C om
=64��x2����8��x��2��
=��2x2+16x��
�䷽�ã�S=��2��x��4��2+32��
���ԣ���x=4ʱ��S�����ֵ32��



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
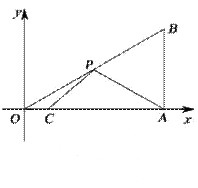
��ͼ����ƽ��ֱ������ϵ�У�Rt��OAB�Ķ���A��x����������ϣ�����B������Ϊ��3��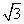 ������C������Ϊ��
������C������Ϊ��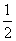 ��0������PΪб��OB�ϵ�һ���㣬��PA��PC����СֵΪ ��
��0������PΪб��OB�ϵ�һ���㣬��PA��PC����СֵΪ ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
��ͼ����֪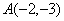 ��
��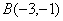 ��
��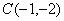 ��ƽ��ֱ������ϵ�����㣮
��ƽ��ֱ������ϵ�����㣮
��1�����㻭�� ABC����ԭ��O�ԳƵ�
ABC����ԭ��O�ԳƵ� A1B1C1 ��
A1B1C1 ��
��2����д����A����y��ԳƵĵ�A2�����꣮������A2����ƽ��h����λ��ʹ������ A1B1C1�ڲ���ָ��h��ȡֵ��Χ��
A1B1C1�ڲ���ָ��h��ȡֵ��Χ��
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com