D
分析:①∠B=90°,则cosA+cosC=4,②∠C=90°,则8cosB+coA=4,根据锐角三角函数的定义,设sinA=x,代入求出x,即可求出答案.
解答:①∠B=90°,则cosA+cosC=4不成立;
②∠C=90°,则8cosB+cosA=4,
∵cosB=sinA=

,
∴8sinA+cosA=4,
设sinA=x,则8x+cosA=4,
cosA=4-8x,
∵sinA=

,cosA=

,
∴sin
2A+cos
2A=

+
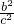
=
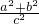
=1,
即sin
2A+cos
2A=1,
∴(4-8x)
2+x
2=1,
65x
2-64x+15=0,
(5x-3)(13x-5)=0,
∴x
1=

,x
2=

,
当x=

时,cosA=4-8x<0,舍去,
∴sinB=

,
∴a:b:c=5:12:13.
故选D.
点评:本题主要考查对解直角三角形,锐角三角函数的定义等知识点的理解和掌握,能正确分类求出所有情况是解此题的关键.

 ,
, ,cosA=
,cosA= ,
, +
+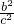 =
=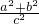 =1,
=1, ,x2=
,x2= ,
, 时,cosA=4-8x<0,舍去,
时,cosA=4-8x<0,舍去, ,
,

 阅读快车系列答案
阅读快车系列答案