练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    【题目】如图，已知二次函数y=﹣+bx+c的图象经过A（2，0）、B（0，﹣6）两点．

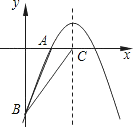
    （1）求这个二次函数的解析式；

    （2）设该二次函数的对称轴与x轴交于点C，连接BA、BC，求△ABC的面积．

    【答案】（1）y=﹣+4x﹣6（2）6

    【解析】

    试题分析：（1）二次函数图象经过A（2，0）、B（0，﹣6）两点，两点代入y=﹣+bx+c，算出b和c，即可得解析式．（2）先求出对称轴方程，写出C点的坐标，计算出AC，然后由面积公式计算值．

    解：（1）把A（2，0）、B（0，﹣6）代入y=﹣+bx+c，

    得：

    解得，

    ∴这个二次函数的解析式为y=﹣+4x﹣6．

    （2）∵该抛物线对称轴为直线x=﹣=4，

    ∴点C的坐标为（4，0），

    ∴AC=OC﹣OA=4﹣2=2，

    ∴S△ABC=×AC×OB=×2×6=6．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    【题目】先阅读，再回答问题：

    要比较代数式A、B的大小，可以作差A-B，比较差的取值，当A-B>0时，有A>B；当A-B=0时，有A=B；当A-B<0时，有A<B.”例如，当a<0时，比较的大小.可以观察因为当a<0时，-a>0，所以当a<0时， .
    （1）已知M=,比较M、N的大小关系.

    （2）某种产品的原料提价,因而厂家决定对于产品进行提价,现有三种方案:

    方案1：第一次提价p%,第二次提价q%;

    方案2：第一次提价q%,第二次提价p%;

    方案3：第一、二次提价均为

    如果设原价为a元，请用含a、p、q的式子表示提价后三种方案的价格.

    方案1： ；方案2： ；方案3：_______

    如果p,q是不相等的正数,三种方案哪种提价最多?

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】已知：|a﹣1|+|b+2|=0，求2a+b的值．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】二次函数y＝x2﹣2x﹣3的开口方向是向__．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，M是△ABC的边BC的中点，AN平分∠BAC，BN⊥AN于点N，延长BN交AC于点D，已知AB=10，BC=15，MN=3

    （1）求证：BN=DN；

    （2）求△ABC的周长．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】某市按如下规定收取每月煤气费：用煤气如果不超过60立方米，每立方米按1元收费，如果超过60立方米，超过部分按每月1.5元收费．已知12月份某用户的煤气费平均每立方米1.2元，那么12月份该用户用煤气_______立方米．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】下列命题中正确的是（ ）

    A．有两条边相等的两个等腰三角形全等

    B．两腰对应相等的两个等腰三角形全等

    C．两角对应相等的两个等腰三角形全等

    D．一边对应相等的两个等边三角形全等

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，在△ABC中，AB=BC，D、E、F分别是BC、AC、AB边上的中点．

    （1）求证：四边形BDEF是菱形；

    （2）若AB=12cm，求菱形BDEF的周长．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，在等腰Rt△ABC中，∠C=90°，AC=8，F是AB边上的中点，点D，E分别在AC，BC边上运动，且保持AD=CE．连接DE，DF，EF．在此运动变化的过程中，下列结论：

    ①△DFE是等腰直角三角形；

    ②四边形CDFE不可能为正方形，

    ③DE长度的最小值为4；

    ④四边形CDFE的面积保持不变；

    ⑤△CDE面积的最大值为8．

    其中正确的结论是（ ）

    A．①②③ B．①④⑤ C．①③④ D．③④⑤

    查看答案和解析>>

    同步练习册答案