
����Ŀ��CPIָ�������Ѽ۸�ָ������ӳ�����ͥ����������Ʒ������ļ۸�ˮƽ�ı䶯�����CPI���ǵ�����һ���̶��ܵ����������غ��������ص�Ӱ�죮���ݱ�����2015����2016��CPI�ǵ��ʵ�ͳ��ͼ�е���Ϣ�����ж�2015��1��8�·���2016��1��8�·ݣ�ͬ�·ݱȽ�CPI�ǵ����½������·����£������ͼ���ṩ����Ϣ��Ԥ��������2016����ļ���CPI�ǵ��ʱ仯������ �� ���Ԥ�������� �� 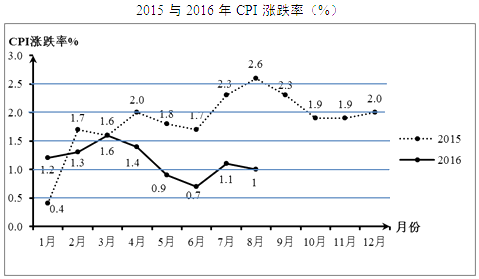
���𰸡���8���ȼ�������2015��9��12�·�CPI�ǵ����ȼ�����������Ԥ��������2016����ļ���CPI�ǵ��ʱ仯�������ȼ�����
���������⣺�ɺ���ͼ���֪��2015��1��8�·���2016��1��8�·ݣ�ͬ�·�CPI�ǵ���8�·����2.6%��1%=1.6%�� ��ͬ�·ݱȽ�CPI�ǵ����½������·���8�£�
����ͼ���ṩ����Ϣ��Ԥ��������2016����ļ���CPI�ǵ��ʱ仯�������ȼ�������
Ԥ��������2015��1��8�·���2016��1��8�·ݣ�ͬ�·�CPI�ǵ��ʻ�������һ�£���2015��9��12�·�CPI�ǵ����ȼ�������
��Ԥ��������2016����ļ���CPI�ǵ��ʱ仯�������ȼ�������
���Դ��ǣ�8���ȼ�������2015��9��12�·�CPI�ǵ����ȼ�����������Ԥ��������2016����ļ���CPI�ǵ��ʱ仯�������ȼ�������
�����㾫����������Ĺؼ��������⺯����ͼ������֪ʶ�����պ�����ͼ������ֱ������ϵ�е�һϵ�е���ɣ�ͼ����ÿһ�����꣨x��y�������˺�����һ�Զ�Ӧֵ�����ĺ�����x��ʾ�Ա�����ij��ֵ��������y��ʾ������Ӧ�ĺ���ֵ��



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��һ��ܵ���ͼ1��ʾ�������ı���ABCD�Ǿ��Σ�O��AC���е㣬�ܵ���AB��BC��CD��DA��OA��OB��OC��OD��ɣ���BC���е�M ��������һ̨��λ������һ���������ڹܵ��������н����Թܵ����м�⣮��������н���ʱ��Ϊx���������붨λ����֮��ľ���Ϊy����ʾy��x�ĺ�����ϵ��ͼ�������ͼ2��ʾ��������˵��н�·�߿���Ϊ�� ��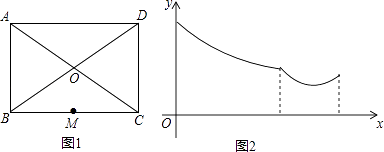
A.A��O��D
B.B��O��D
C.A��B��O
D.A��D��O
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����ͼ��һ�κ��� ![]() �뷴��������
�뷴�������� ![]() ��ͼ���ڵ�һ���Ľ���ΪA��1��n����
��ͼ���ڵ�һ���Ľ���ΪA��1��n���� 
��1����m��n��ֵ��
��2����һ�κ�����ͼ����x�ύ�ڵ�B������OA�����BAO�Ķ�����
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������һ���仯����������������x��y���������x��ÿһ��ֵ��y����Ψһȷ����ֵ������Ӧ����ô��˵y��x�ĺ���������y=f��x�����ں���y=f��x���У����Ա���x=aʱ����Ӧ�ĺ���ֵy���Ա�ʾΪf��a����
���磺����f��x��=x2��2x��3����x=4ʱ��f��4��=42��2��4��3=5��ƽ��ֱ������ϵxOy�У����ں��������������¶��壺
�������y=f��x����a��x��b�ķ�Χ�ڶ�Ӧ��ͼ����һ���������ϵ����ߣ�����f��a����f��b����0����ô����y=f��x����a��x��b�ķ�Χ������㣬������c��a��c��b����ʹf��c��=0����c���������������㣬cҲ�Ƿ���f��x��=0��a��x��b��Χ�ڵĸ���
���磺���κ���f��x��=x2��2x��3��ͼ����ͼ1��ʾ��
�۲��֪��f����2����0��f��1����0����f����2����f��1����0�����Ժ���f��x��=x2��2x��3�ک�2��x��1��Χ������㣮����f����1��=0�����ԣ���1��f��x��=x2��2x��3����㣬��1Ҳ�Ƿ���x2��2x��3=0�ĸ���
��1���۲캯��y1=f��x����ͼ��2���ش��������⣺
��f��a��f��b�� 0����������������=����
����a��x��b��Χ��y1=f��x�������ĸ����� ��
��2����֪����y2=f��x��=�� ![]() �����Ϊx1 �� x2 �� ��x1��1��x2 ��
�����Ϊx1 �� x2 �� ��x1��1��x2 ��
�������Ϊx1 �� x2����a��ʾ����
����ƽ��ֱ������xOy�У���x����A��B�����ʾ���������x1 �� x2 �� �� PΪ�߶�AB�ϵ�һ�����㣨P����A��B���㲻�غϣ�����x���Ϸ����ȱߡ�APM�͵ȱߡ�BPN�����߶�MN���е�ΪQ����a����������������y2�ı���ʽ��ֱ��д���߶�PQ����ȡֵ��Χ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ƽ��ֱ������ϵ�еĵ�������ƽ�ƣ���x�᷽��ƽ�Ƶ�����Ϊa������Ϊ��������Ϊ����ƽ��|a|����λ������y�᷽��ƽ�Ƶ�����Ϊb������Ϊ��������Ϊ����ƽ��|b|����λ���������������{a��b}������һƽ�Ƶġ�ƽ���������涨��ƽ������{a��b}�롰ƽ������{c��d}�ļӷ����㷨��Ϊ{a��b}+{c��d}={a+c��b+d}��
��1��������P�������M��1��1�����������ա�ƽ������{2��0}ƽ�Ƶ�N���ٰ��ա�ƽ������{1��2}ƽ�Ƶ�G���γɡ�MNG�����N������Ϊ �� ��G������Ϊ ��
��2��������P������ԭ��������Ȱ��ա�ƽ������mƽ�Ƶ�B���ٰ��ա�ƽ������nƽ�Ƶ�C������ա�ƽ������qƽ�ƻص���O������OBC�ס�MNG���ڣ�1���е������Σ��������Ʊ�Ϊ2��1ʱ������ֱ��д����ƽ������m �� n �� q ��
��3���ڣ�1������2����ǰ���£�������ƽ��ֱ������ϵ�л�����OBC���MNG��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����Ƕ��κ���y=ax2+bx+c�IJ���x��y�Ķ�Ӧֵ��
x | �� | ��1 | �� | 0 |
| 1 |
| 2 |
| 3 | �� |
y | �� | m |
| ��1 |
| ��2 |
| ��1 |
| 2 | �� |
��1�����κ���ͼ��Ŀ����� �� ���������� �� m��ֵΪ��
��2����x��0ʱ��y��ȡֵ��Χ����
��3����������y=ax2+bx+c�Ķ�����ֱ��y=x+n���·�ʱ��n��ȡֵ��Χ�� ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��ij�����ߵĶԳ���Ϊֱ��x=2����E�Ǹ������߶��㣬��������y�ύ�ڵ�C������C��CD��x�ᣬ�������߽��ڵ�B����Գ��ύ�ڵ�D����A�ǶԳ�����һ�㣬����AC��AB������ABC�ǵȱ������Σ���ͼ����Ӱ����ͼ�ε����֮���� �� 
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ������ABCD��AB=12cm��BC=6cm����P��AB�ߴӵ�A��ʼ��2cm/����ٶ��ƶ�����Q��DA�ߴ�D��1cm/����ٶ��ƶ�����P��Qͬʱ��������t��ʾ�ƶ�ʱ�䣨0��t��6������t��ֵʱ����APQ���ABC���ƣ� 
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��������y= ![]() x2+bx+c��x�ύ��A��B���㣬��y�ύ�ڵ�C����Գ��ύ�������ڵ�D����x���ڵ�E����֪OB=OC=6��
x2+bx+c��x�ύ��A��B���㣬��y�ύ�ڵ�C����Գ��ύ�������ڵ�D����x���ڵ�E����֪OB=OC=6��
��1���������ߵĽ���ʽ����D�����ꣻ
��2������BD��FΪ��������һ���㣬����FAB=��EDBʱ�����F�����ꣻ
��3��ƽ����x���ֱ�߽���������M��N���㣬���߶�MNΪ�Խ���������MPNQ������P��x���ϣ���PQ= ![]() MNʱ�������ζԽ���MN�ij���
MNʱ�������ζԽ���MN�ij���
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com