
分析 根据弧长公式和圆的周长公式可以求得60°的圆心角所对的弧长与圆周长的比值,由扇形面积公式和圆的面积公可以求得圆心角是45°的扇形的面积与圆的面积的比值.
解答 解:由题意可得,
设圆的半径为r,
则60°的圆心角所对的弧长是圆周长的:$\frac{\frac{60×πr}{180}}{2πr}$=$\frac{1}{6}$,
圆心角是45°的扇形占圆的面积的:$\frac{\frac{45×π{r}^{2}}{360}}{π{r}^{2}}$=$\frac{1}{8}$,
故答案为:$\frac{1}{6}$,$\frac{1}{8}$.
点评 本题考查扇形面积的计算、弧长的计算,解答本题的关键是明确弧长公式是$\frac{nπr}{180}$,扇形的面积公式是$\frac{n{πr}^{2}}{360}$.


科目:初中数学 来源: 题型:选择题
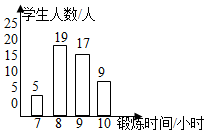 小文统计了本班同学一周的体育锻练情况,并绘制了直方图
小文统计了本班同学一周的体育锻练情况,并绘制了直方图| A. | ①② | B. | ②③ | C. | ③④ | D. | ①④ |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 0.4 | B. | 0.6 | C. | 0.5 | D. | 0.65 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
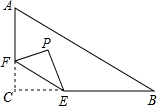 如图,在Rt△ABC中,∠C=90°,AC=6,BC=8,点F在边AC上,点E为边BC上的动点,将△CEF沿直线EF翻折,点C落在点P处.
如图,在Rt△ABC中,∠C=90°,AC=6,BC=8,点F在边AC上,点E为边BC上的动点,将△CEF沿直线EF翻折,点C落在点P处.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com