
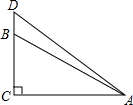
 如图,在一棵树的10米高B处有三只猴子,第一只猴子爬下树走到离树20米处的池塘A处,第二只猴子直接从B处跃到A处,第三只爬到树顶D后直接跃到A处,距离以直线计算,假设其中两只猴子所经过的距离相等.
如图,在一棵树的10米高B处有三只猴子,第一只猴子爬下树走到离树20米处的池塘A处,第二只猴子直接从B处跃到A处,第三只爬到树顶D后直接跃到A处,距离以直线计算,假设其中两只猴子所经过的距离相等.| BC2+AC2 |
| 102+202 |
| 5 |
| 5 |


 学练快车道快乐假期寒假作业系列答案
学练快车道快乐假期寒假作业系列答案科目:初中数学 来源: 题型:
查看答案和解析>>
科目:初中数学 来源:2011-2012学年江苏省江阴市周庄中学八年级上学期期中数学试卷(带解析) 题型:解答题
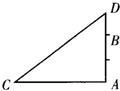
如图,在一棵树的10 高B处有2只猴子,一只猴子爬到树下走到离树20
高B处有2只猴子,一只猴子爬到树下走到离树20 处的池塘A处,另一只爬到树顶D后直接跳跃到A处,距离以直线计算,如果两只猴子所经过的距离相等,求这棵树高.
处的池塘A处,另一只爬到树顶D后直接跳跃到A处,距离以直线计算,如果两只猴子所经过的距离相等,求这棵树高.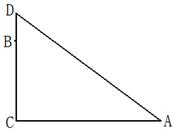
查看答案和解析>>
科目:初中数学 来源:2013届江苏省江阴市八年级上学期期中数学试卷(解析版) 题型:解答题
如图,在一棵树的10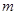 高B处有2只猴子,一只猴子爬到树下走到离树20
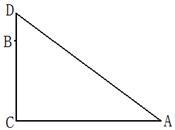
高B处有2只猴子,一只猴子爬到树下走到离树20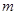 处的池塘A处,另一只爬到树顶D后直接跳跃到A处,距离以直线计算,如果两只猴子所经过的距离相等,求这棵树高.
处的池塘A处,另一只爬到树顶D后直接跳跃到A处,距离以直线计算,如果两只猴子所经过的距离相等,求这棵树高.
查看答案和解析>>
科目:初中数学 来源: 题型:
如图,在一棵树的10米高B处有三只猴子,第一只猴子爬下树走到离树20米处的池塘A处,第二只猴子直接从B处跃到A处,第三只爬到树顶D后直接跃到A处,距离以直线计算,假设其中两只猴子所经过的距离相等.
(1)求第二只猴子经过的直线距离;
(2)求这棵树的高度.
 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com