

���� ��1���ѵ�P��1��2������y=$\frac{k}{x}$���ɽ�����⣮
��2���ٸ���S��OEF=S�ı���OEFA-S��OFA=S��EOC+S�ı���ECAF-S��FOA����ΪS��EOC=S��FOA���ɴ˼��ɽ�����⣮
����ͼ2�У���EM��OA��M�����âٽ����г����̼��ɽ�����⣮
��� �⣺��1����ͼ1�У�
�������P���꣨1��2����
��E��P�غ�ʱ��P��1��2������y=$\frac{k}{x}$��k=2��
��2���١�S��OEF=S�ı���OEFA-S��OFA
=S��EOC+S�ı���ECAF-S��FOA��
��S��EOC=S��FOA��
��S��EOF=S�ı���ECAF��
����ͼ2�У���EM��OA��M��
���E���꣨m��2������S��OEF=2S��PEF��
��S�ı���FAME=2S��PEF��
��$\frac{1}{2}$��2+2m����m-1��=2��$\frac{1}{2}$��m-1����2m-2����
��m=3��1��
��k��2��m=1�������⣬
��m=3��
���E���꣨3��2����
���� ���⿼�鷴����������һ�κ����Ľ������⣬���շ����������ı���ϵ��k�ļ��������ǽ���Ĺؼ��������п��������ͣ�



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
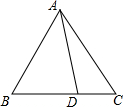 ��ͼ���ڡ�ABC�У�AB=AC����DΪһ����һ�㣬����������������BC����ȷ��E��ʹCE=BD�����������������˵�����ɣ�
��ͼ���ڡ�ABC�У�AB=AC����DΪһ����һ�㣬����������������BC����ȷ��E��ʹCE=BD�����������������˵�����ɣ��鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
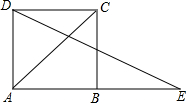 ��ͼ���ӳ�������ABCD�ı�AB��E��ʹBE=AC�����E=��������
��ͼ���ӳ�������ABCD�ı�AB��E��ʹBE=AC�����E=��������| A�� | 45�� | B�� | 30�� | C�� | 22.5�� | D�� | 15�� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | AB��CD AD=BC | B�� | ��A=��B��C=��D | C�� | AB=CD AD=BC | D�� | AB=AD CB=CD |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
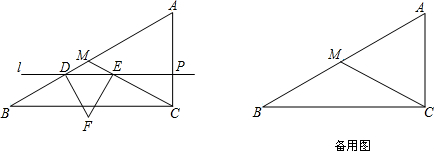
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
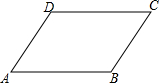 ��ͼ����ƽ���ı���ABCD�У������A=50�㣬���C=��������
��ͼ����ƽ���ı���ABCD�У������A=50�㣬���C=��������| A�� | 40�� | B�� | 50�� | C�� | 130�� | D�� | 150�� |
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com