
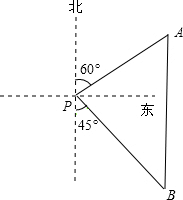
 如图,一艘海轮位于灯塔P的北偏东60°方向,距离灯塔86n mile的A处,它沿正南方向航行一段时间后,到达位于灯塔P的南偏东45°方向上的B处,此时,B处与灯塔P的距离约为102n mile.(结果取整数,参考数据:$\sqrt{3}$≈1.7,$\sqrt{2}$≈1.4)
如图,一艘海轮位于灯塔P的北偏东60°方向,距离灯塔86n mile的A处,它沿正南方向航行一段时间后,到达位于灯塔P的南偏东45°方向上的B处,此时,B处与灯塔P的距离约为102n mile.(结果取整数,参考数据:$\sqrt{3}$≈1.7,$\sqrt{2}$≈1.4) 分析 根据题意得出∠MPA=∠PAD=60°,从而知PD=AP•sin∠PAD=43$\sqrt{3}$,由∠BPD=∠PBD=45°根据BP=$\frac{PD}{sin∠B}$,即可求出即可.
解答 解:过P作PD⊥AB,垂足为D,
∵一艘海轮位于灯塔P的北偏东60°方向,距离灯塔86n mile的A处,
∴∠MPA=∠PAD=60°,
∴PD=AP•sin∠PAD=86×$\frac{\sqrt{3}}{2}$=43$\sqrt{3}$,
∵∠BPD=45°,
∴∠B=45°.
在Rt△BDP中,由勾股定理,得
BP=$\frac{PD}{sin∠B}$=$\frac{43\sqrt{3}}{\frac{\sqrt{2}}{2}}$=43$\sqrt{3}$×$\sqrt{2}$≈102(n mile).
故答案为:102.
点评 此题主要考查了方向角含义,勾股定理的运用,正确记忆三角函数的定义得出相关角度是解决本题的关键.


 教育世家状元卷系列答案
教育世家状元卷系列答案 黄冈课堂作业本系列答案
黄冈课堂作业本系列答案 单元加期末复习先锋大考卷系列答案
单元加期末复习先锋大考卷系列答案科目:初中数学 来源: 题型:解答题
 如图,一次函数y=-$\frac{\sqrt{3}}{3}$x+b的图象与x轴交于点为A(-4$\sqrt{3}$,0),与y轴交于点为B.
如图,一次函数y=-$\frac{\sqrt{3}}{3}$x+b的图象与x轴交于点为A(-4$\sqrt{3}$,0),与y轴交于点为B.查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:填空题
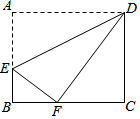 如图,矩形ABCD中,点E在边AB上,将一边AD折叠,使点A恰好落在边BC的点F处,折痕为DE,若AB=8,BF=4,则BC=10cm.
如图,矩形ABCD中,点E在边AB上,将一边AD折叠,使点A恰好落在边BC的点F处,折痕为DE,若AB=8,BF=4,则BC=10cm.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
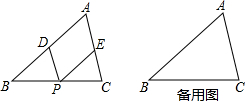 在△ABC中,点P是BC上一动点(与B、C不重合),过点P作PD∥AC交AB于D.作PE∥AB交AC于E,则四边形AEPD是平行四边形.
在△ABC中,点P是BC上一动点(与B、C不重合),过点P作PD∥AC交AB于D.作PE∥AB交AC于E,则四边形AEPD是平行四边形.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
| 甲 | 乙 | 丙 | 丁 | |
| $\overline{x}$ | 1′05″33 | 1′04″26 | 1′04″26 | 1′07″29 |
| S2 | 1.1 | 1.1 | 1.3 | 1.6 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 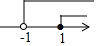 | B. |  | C. | 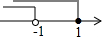 | D. | 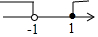 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | -$\frac{5}{4}$ | B. | -$\frac{1}{4}$ | C. | -$\frac{3}{4}$ | D. | 0 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com