
如图1,已知抛物线 与x轴交于A、B两点(点A在点B的左侧),与y轴交于点C,且OB =" 2OA" = 4.
与x轴交于A、B两点(点A在点B的左侧),与y轴交于点C,且OB =" 2OA" = 4.

(1)求该抛物线的函数表达式;
(2)设P是(1)中抛物线上的一个动点,以P为圆心,R为半径作⊙P,求当⊙P与抛物线的对称轴l及x轴均相切时点P的坐标.
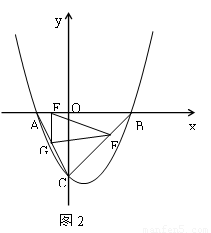
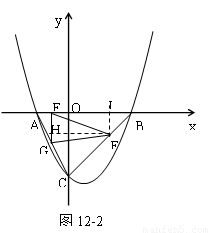
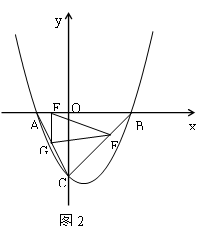
(3)动点E从点A出发,以每秒1个单位长度的速度向终点B运动,动点F从点B出发,以每秒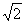 个单位长度的速度向终点C运动,过点E作EG//y轴,交AC于点G(如图2).若E、F两点同时出发,运动时间为t.则当t为何值时,△EFG的面积是△ABC的面积的
个单位长度的速度向终点C运动,过点E作EG//y轴,交AC于点G(如图2).若E、F两点同时出发,运动时间为t.则当t为何值时,△EFG的面积是△ABC的面积的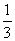 ?
?
(1)抛物线为 (2)满足条件的点P的坐标为P1(
(2)满足条件的点P的坐标为P1(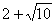 ,
, )、P2(
)、P2(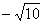 ,
, )、P3(
)、P3( ,
, )、P4(
)、P4(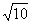 ,
, )(3)当t = 1时,△EFG的面积是△ABC的面积的
)(3)当t = 1时,△EFG的面积是△ABC的面积的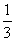
【解析】
试题分析:(1)解:∵OB=2OA=4
∴A(–2,0)、B(4,0)
由已知得:

解得: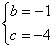
所求抛物线为
(2)解法一:当点P在第一象限时,
过点P作PQ⊥l于Q,作PR⊥x轴于R
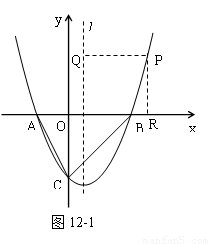
⊙P与x轴、直线l都相切,
∴PQ=PR
由(1)知抛物线的对称轴l为x = 1,设P(x,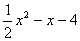 )
)
则PQ = x–1,PR = 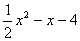
∴x–1 = 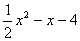 ,解得:
,解得: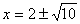 (其中
(其中 舍去)
舍去)
∴PR =" PQ" = x–1=
∴P(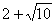 ,
, )
)
同理,当点P在第二象限时,可得P(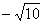 ,
, )
)
当点P在第三象限时,可得P( ,
, )
)
当点P在第四象限时,可得P(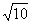 ,
, )
)
综上述,满足条件的点P的坐标为P1(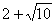 ,
, )、P2(
)、P2(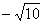 ,
, )、P3(
)、P3( ,
, )、P4(
)、P4(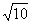 ,
, )
)
解法二:由已知得点P也在由对称轴l及x轴所组成的角的平分线所在的直线m上

当直线m过一、三、四象限时,设直线m与y轴交于N,对称轴l与x轴交于M
由(1)知直线l为x = 1
故M(1,0)
∵∠OMN =45º=∠ONM
∴ON =" OM" = 1
∴N(0,–1)
∴直线m为:y = x–1
解方程组
得:

∴点P的坐标为(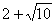 ,
, )或(
)或( ,
, )
)
当直线m经过一、二、四象限时,
同理可得点P的坐标为(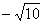 ,
, )或(
)或(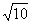 ,
, )
)
∴点P的坐标为P1(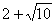 ,
, )、P2(
)、P2(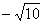 ,
, )、P3(
)、P3( ,
, )、P4(
)、P4( ,
, )
)
(3)解:过点F作FH⊥EG于点H,作FJ⊥x轴于J
由(1)知点C的坐标为(0,–4)
∴OB=OC=4
∵∠OBC=∠OCB = 45º
∴FJ=BJ=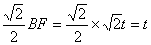
∴F(4–t,t)
∵AE = t,∴E(–2 + t,0)
∴A(–2,0)、C(0,–4)
∴直线AC为:y =–2x–4
把x =–2 + t代入得:y =–2t,∴G(–2 + t,–2t)
∴EG = 2t,FH = (4–t )–(–2 + t ) = 6–2t
∴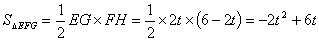
∵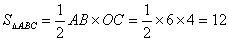
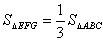
∴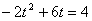 ,解得
,解得 ,
,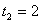
∵当t = 2时,G(0,–4),E(0,0),此时EG与OC重合,不合题意,舍去
∴当t = 1时,△EFG的面积是△ABC的面积的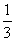 .
.
考点:二次函数和动点问题
点评:本题难度较大,主要考查学生对二次函数解决动点问题综合运用能力,动点为中考常考题型,要求学生注意培养数形结合思想,培养综合分析归纳能力,并运用到考试中去。


科目:初中数学 来源: 题型:
如图23,已知抛物线![]() 与
与![]() 轴相交于A、B两点,其对称轴为直线
轴相交于A、B两点,其对称轴为直线![]() ,且与x轴交于点D,AO=1.
,且与x轴交于点D,AO=1.
1.填空:![]() =_______。
=_______。![]() =_______,点B的坐标为(_______,_______):
=_______,点B的坐标为(_______,_______):
2.若线段BC的垂直平分线EF交BC于点E,交![]() 轴于点F.求FC的长;
轴于点F.求FC的长;
3.探究:在抛物线的对称轴上是否存在点P,使⊙P与![]() 轴、直线BC都相切?若存在,请求出点P的坐标;若不存在,请说明理由。
轴、直线BC都相切?若存在,请求出点P的坐标;若不存在,请说明理由。

查看答案和解析>>
科目:初中数学 来源: 题型:
如图1,已知抛物线![]() 与x轴交于点A和点B,与y轴相交于点C.
与x轴交于点A和点B,与y轴相交于点C.
1.求A、B、C三点的坐标
2.点D为射线CB上的一动点(点D、B不重合),过点B作x轴的垂线BE与以点D为顶点的抛物线y=(x-t)2+h相交于点E,从△ADE和△ADB中任选一个三角形,求出当其面积等于△ABE的面积时的t的值;(友情提示:1、只选取一个三角形求解即可;2、若对两个三角形都作了解答,只按第一个解答给分.)
3.如图2,若点P是直线![]() 上的一个动点,点Q是抛物线上的一个动点,若以点O,C,P和Q为顶点的四边形为直角梯形,求相应的点P的坐标.
上的一个动点,点Q是抛物线上的一个动点,若以点O,C,P和Q为顶点的四边形为直角梯形,求相应的点P的坐标.
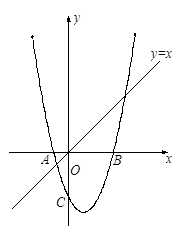
查看答案和解析>>
科目:初中数学 来源:2011年初中毕业升学考试(广西区南宁卷)数学 题型:解答题
(本题满分9分)
如图11,已知抛物线 与x 轴交于两点A、B,其顶点为C.
与x 轴交于两点A、B,其顶点为C.
(1)对于任意实数m,点M(m,-2)是否在该抛物线上?请说明理由;
(2)求证:△ABC是等腰直角三角形;
(3)已知点D在x轴上,那么在抛物线上是否存在点P,使得以B、C、D、P为顶点的四边形是 平行四边形?若存在,求点P的坐标;若不存在,请说明理由.
平行四边形?若存在,求点P的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源:2013年广东省广州市南沙区中考一模数学试卷(带解析) 题型:解答题
如图1,已知抛物线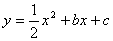 与x轴交于A、B两点(点A在点B的左侧),与y轴交于点C,且OB =" 2OA" = 4.
与x轴交于A、B两点(点A在点B的左侧),与y轴交于点C,且OB =" 2OA" = 4.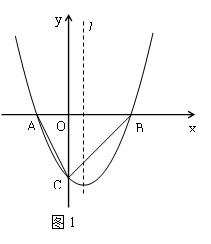
(1)求该抛物线的函数表达式;
(2)设P是(1)中抛物线上的一个动点,以P为圆心,R为半径作⊙P,求当⊙P与抛物线的对称轴l及x轴均相切时点P的坐标.
(3)动点E从点A出发,以每秒1个单位长度的速度向终点B运动,动点F从点B出发,以每秒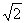 个单位长度的速度向终点C运动,过点E作EG//y轴,交AC于点G(如图2).若E、F两点同时出发,运动时间为t.则当t为何值时,△EFG的面积是△ABC的面积的
个单位长度的速度向终点C运动,过点E作EG//y轴,交AC于点G(如图2).若E、F两点同时出发,运动时间为t.则当t为何值时,△EFG的面积是△ABC的面积的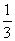 ?
?
查看答案和解析>>
科目:初中数学 来源:2011-2012学年湖北武汉部分学校九年级5月供题调研数学试卷(解析版) 题型:解答题
如图1,已知抛物线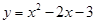 与x轴交于点A和点B,与y轴相交于点C.
与x轴交于点A和点B,与y轴相交于点C.
1.求A、B、C三点的坐标
2.点D为射线CB上的一动点(点D、B不重合),过点B作x轴的垂线BE与以点D为顶点的抛物线y=(x-t)2+h相交于点E,从△ADE和△ADB中任选一个三角形,求出当其面积等于△ABE的面积时的t的值;(友情提示:1、只选取一个三角形求解即可;2、若对两个三角形都作了解答,只按第一个解答给分.)
3.如图2,若点P是直线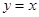 上的一个动点,点Q是抛物线上的一个动点,若以点O,C,P和Q为顶点的四边形为直角梯形,求相应的点P的坐标.
上的一个动点,点Q是抛物线上的一个动点,若以点O,C,P和Q为顶点的四边形为直角梯形,求相应的点P的坐标.
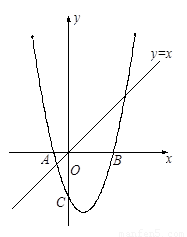
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com