
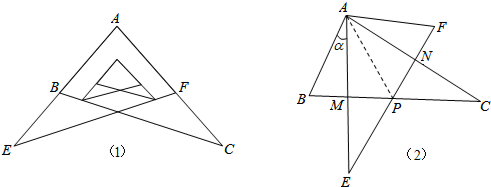
某校九年级学习小组在探究学习过程中,用两块完全相同的且含60°角的直角三角板ABC与AFE按如图
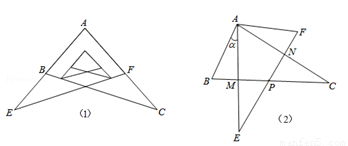
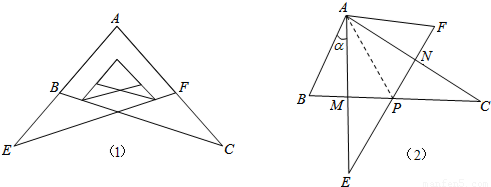
(1)所示位置放置放置,现将Rt△AEF绕A点按逆时针方向旋转角α(0°<α<90°),如图(2),AE与BC交于点M,AC与EF交于点N,BC与EF交于点P.
(1)求证:AM=AN;
(2)当旋转角α=30°时,四边形ABPF是什么样的特殊四边形?并说明理由.
解:(1)证明:∵用两块完全相同的且含60°角的直角三角板ABC与AFE按如图(1)所示位置放置放置,现将Rt△AEF绕A点按逆时针方向旋转角α(0°<α<90°),
∴AB=AF,∠BAM=∠FAN。
∵在△ABM和△AFN中,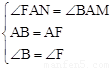 ,
,
∴△ABM≌△AFN(ASA)。
∴AM=AN。
(2)当旋转角α=30°时,四边形ABPF是菱形。理由如下:
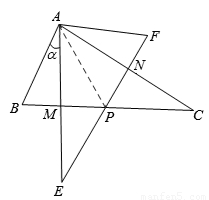
连接AP,
∵∠α=30°,∴∠FAN=30°。∴∠FAB=120°。
∵∠B=60°,∴AF∥BP。∴∠F=∠FPC=60°。
∴∠FPC=∠B=60°。∴AB∥FP。
∴四边形ABPF是平行四边形。
∵AB=AF,∴平行四边形ABPF是菱形。
【解析】(1)根据旋转的性质得出AB=AF,∠BAM=∠FAN,进而得出△ABM≌△AFN得出答案即可。
(2)利用旋转的性质得出∠FAB=120°,∠FPC=∠B=60°,即可得出四边形ABPF是平行四边形,再利用菱形的判定得出答案。


科目:初中数学 来源: 题型:

查看答案和解析>>
科目:初中数学 来源:2013-2014学年江西省九年级3月月考数学试卷(解析版) 题型:解答题
某校九年级学习小组在探究学习过程中,用两块完全相同的且含60°角的直角三角板ABC与AFE按如图(1)所示位置放置放置,现将Rt△AEF绕A点按逆时针方向旋转角α(0°<α<90°),如图(2),AE与BC交于点M,AC与EF交于点N,BC与EF交于点P.
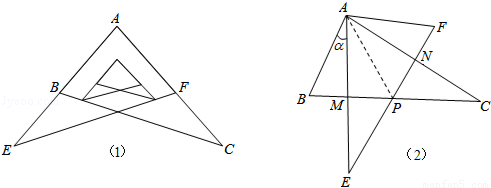
(1)求证:AM=AN;
(2)当旋转角α=30°时,四边形ABPF是什么样的特殊四边形?并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源:2013年湖南省娄底市中考数学试卷(解析版) 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com