
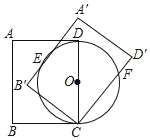
【题目】如图,在矩形ABCD中,AB=10,BC=8,以CD为直径作⊙O.将矩形ABCD绕点C旋转,使所得矩形A′B′CD′的边A′B′与⊙O相切,切点为E,边CD′与⊙O相交于点F,则CF的长为_____.
 新课标快乐提优暑假作业陕西旅游出版社系列答案
新课标快乐提优暑假作业陕西旅游出版社系列答案 暑假衔接培优教材浙江工商大学出版社系列答案
暑假衔接培优教材浙江工商大学出版社系列答案科目:初中数学 来源: 题型:
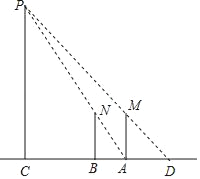
【题目】甲和乙两位同学想测量一下广场中央的照明灯P的高度,如图,当甲站在A处时,乙测得甲的影子长AD正好与他的身高AM相等,接着甲沿AC方向继续向前走,走到点B处时,甲的影子刚好是线段AB,此时测得AB的长为1.2m.已知甲直立时的身高为1.8m,求照明灯的高CP的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校为市体校选拔一名篮球队员![]() 教练对王亮和李刚两名同学进行5次3分投篮测试,每人每次投10个球,下图记录的是这两名同学5次投篮中所投中的个数.
教练对王亮和李刚两名同学进行5次3分投篮测试,每人每次投10个球,下图记录的是这两名同学5次投篮中所投中的个数.
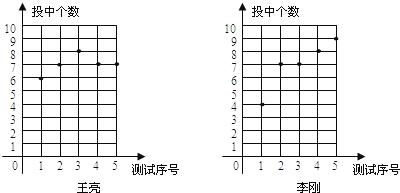
![]() 请你根据图中的数据,填写下表
请你根据图中的数据,填写下表
姓名 | 平均分 | 众数 | 极差 | 方差 |
王亮 | 7 | 7 | ______ |
|
李刚 | 7 | ______ | 5 | ______ |
![]() 你认为谁的成绩比较稳定,为什么?
你认为谁的成绩比较稳定,为什么?
![]() 若你是教练,你打算选谁参赛?请利用以上数据或图中信息简要说明理由.
若你是教练,你打算选谁参赛?请利用以上数据或图中信息简要说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
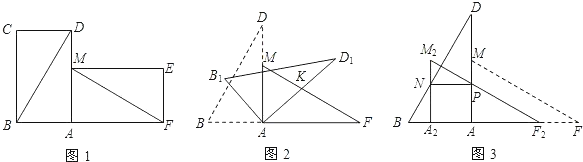
【题目】有两张完全重合的矩形纸片,小亮同学将其中一张绕点A顺时针旋转90°后得到矩形AMEF(如图1),连接BD、MF,若此时他测得BD=8cm,∠ADB=30度.请回答下列问题:(1)试探究线段BD与线段MF的关系,并简要说明理由;
(2)小红同学用剪刀将△BCD与△MEF剪去,与小亮同学继续探究.他们将△ABD绕点A顺时针旋转得△AB1D1,AD1交FM于点K(如图2),设旋转角为β(0°<β<90°),当△AFK为等腰三角形时,请直接写出旋转角β的度数;
(3)若将△AFM沿AB方向平移得到△A2F2M2(如图3),F2M2与AD交于点P,A2M2与BD交于点N,当NP∥AB时,求平移的距离是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线y=-x2+bx+c与x轴交于A、B两点,且B点的坐标为(3,0),经过A点的直线交抛物线于点D (2, 3).
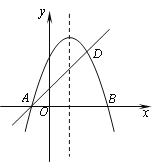
(1)求抛物线的解析式和直线AD的解析式;
(2)过x轴上的点E (a,0) 作直线EF∥AD,交抛物线于点F,是否存在实数a,使得以A、D、E、F为顶点的四边形是平行四边形?如果存在,求出满足条件的a;如果不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示是一个直角三角形的苗圃,由一个正方形花坛和两块直角三角形的草皮组成.如果两个直角三角形的两条斜边长分别为4米和6米,则草皮的总面积为( )平方米.
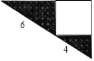
A. 3![]() B. 9 C. 12 D. 24
B. 9 C. 12 D. 24
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在Rt△ABC中,∠ACB=90°,AC=2BC, 将△ABC绕点O按逆时针方向旋转90°得到△DEF,点A,B,C的对应点分别是点D,E,F.请仅用无刻度直尺分别在下面图中按要求画出相应的点(保留画图痕迹).
(1).如图1,当点O为AC的中点时,画出BC的中点N;
(2).如图2, 旋转后点E恰好落在点C,点F落在AC上,点N是BC的中点,画出旋转中心O.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】跳跳一家外出自驾游,出发时油箱里还剩有汽油30升,已知跳跳家的汽车每百千米的平均油耗为12升,设油箱里剩下的油量为y(单位:升),汽车行驶的路程为x(单位:千米).
(1)求y关于x的函数表达式;
(2)若跳跳家的汽车油箱中的油量低于5升时,仪表盘会亮起黄灯警报. 要使邮箱中的存油量不低于5升,跳跳爸爸至多能够行驶多少千米就要进加油站加油?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com