
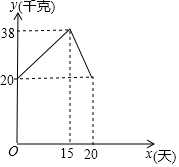
 某粮油超市平时每天都将一定数量的某些品种的粮食进行包装以便出售,已知每天包装江米20千克,为迎接今年5月30日的“端午节”,该超市决定在节前20天增加每天包装江米的质量,包装质量与天数的变化情况如图所示,节日后又恢复到原来每天包装的质量.
某粮油超市平时每天都将一定数量的某些品种的粮食进行包装以便出售,已知每天包装江米20千克,为迎接今年5月30日的“端午节”,该超市决定在节前20天增加每天包装江米的质量,包装质量与天数的变化情况如图所示,节日后又恢复到原来每天包装的质量.分析 (1)观察函数图象找出点的坐标,根据点的坐标利用待定系数法,即可求出在这20天内每天包装江米的质量y(千克)随天数x(x>0且x为正整数)变化的函数关系式;
(2)设日利润为w,结合(1)即可得出w关于x的函数关系式,令w>64,解之即可得出x的取值范围,此题得解.
解答 解:(1)设每天包装江米的质量y(千克)随天数x(x>0且x为正整数)变化的函数关系式为y=kx+b(k≠0),
当0<x≤15时,将(0,20)、(15,38)代入y=kx+b中,
$\left\{\begin{array}{l}{b=20}\\{15k+b=38}\end{array}\right.$,解得:$\left\{\begin{array}{l}{k=1.2}\\{b=20}\end{array}\right.$,
∴此时函数关系式为y=1.2x+20;
当15≤x≤20时,将(15,38)、(20,20)代入y=kx+b中,
$\left\{\begin{array}{l}{15k+b=38}\\{20k+b=20}\end{array}\right.$,解得:$\left\{\begin{array}{l}{k=-3.6}\\{b=92}\end{array}\right.$,
∴此时函数关系式为y=-3.6x+92.
综上所述:y与x之间的函数关系式为y=$\left\{\begin{array}{l}{1.2x+20(0<x≤15且x为正整数)}\\{-3.6x+92(15≤x≤20且x为正整数)}\end{array}\right.$.
(2)设日利润为w,
根据题意得:当0<x≤15时,w=(12-9.5-0.5)(1.2x+20)=2.4x+40;
当15≤x≤20时,w=(12-9.5-0.5)(-3.6x+92)=-7.2x+184.
令2.4x+40>64,
解得:x>10,
∴x=11、12、13、14、15;
令-7.2x+184>64,
解得:x<$\frac{50}{3}$,
∴x=15、16.
∴在这20天中有6天销售江米的利润大于64元.
点评 本题考查了一次函数的应用、待定系数法求一次函数解析式以及解一元一次不等式,解题的关键是:(1)根据点的坐标,利用待定系数法求出一次函数关系式;(2)通过解一元一次不等式找出x的取值范围.


科目:初中数学 来源: 题型:解答题
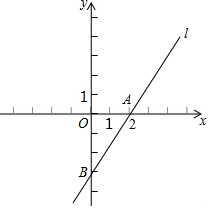 如图,在平面直角坐标系xOy中,过点A(2,0)的直线l:y=mx-3与y轴交于点B.
如图,在平面直角坐标系xOy中,过点A(2,0)的直线l:y=mx-3与y轴交于点B.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 12×105 | B. | 1.2×106 | C. | 1.2×105 | D. | 0.12×105 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
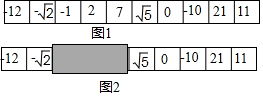 如图1,一张纸条上依次写有10个数,如图2,一卡片每次可以盖住纸条上的3个数,那么随机地用卡片盖住的3个数中有且只有一个是负数的概率$\frac{1}{2}$.
如图1,一张纸条上依次写有10个数,如图2,一卡片每次可以盖住纸条上的3个数,那么随机地用卡片盖住的3个数中有且只有一个是负数的概率$\frac{1}{2}$.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
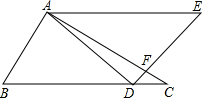 将一副三角板拼成如图所示的图形,即∠BAC=∠ADE=90°,∠DAE=∠E=45°,∠C=30°,∠B=60°,DE与AC相交于点F.
将一副三角板拼成如图所示的图形,即∠BAC=∠ADE=90°,∠DAE=∠E=45°,∠C=30°,∠B=60°,DE与AC相交于点F.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 7.38×104元 | B. | 73.8×105元 | C. | 7.38×106元 | D. | 0.738×106元 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 这一批零件的质量全体是总体 | |
| B. | 从中抽取的10件零件是总体的一个样本 | |
| C. | 这一批零件的长度的全体是总体 | |
| D. | 每一个零件的质量为个体 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | ∠1=50°,∠2=40° | B. | ∠1=50°,∠2=50° | C. | ∠1=40°,∠2=40° | D. | ∠1=45°,∠2=45° |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com