
如图,抛物线![]() 过原点O,与x轴交于A,点D(4,2)在该抛物线上,过点D作CD∥x轴,交抛物线于点C,交y轴于点B,连结CO、AD.
过原点O,与x轴交于A,点D(4,2)在该抛物线上,过点D作CD∥x轴,交抛物线于点C,交y轴于点B,连结CO、AD.
1.求抛物线的解析式及点C的坐标
2.将△BCO绕点O按顺时针旋转90°后 再沿x轴对折得到△OEF(点C与点E对应),判断点E是否落在抛物线上,并说明理由;
3.设过点E的直线交OA于点P,交CD边于点Q. 问是否存在点P,使直线PQ分梯形AOCD的面积为1∶3两部分?若存在,求出P点坐标;若不存在,请说明理由.
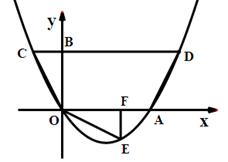
1.![]() ;C(-1,2)
;C(-1,2)
2.点E落在抛物线上. 理由如下:
![]()
由旋转、轴对称的性质知:![]()
![]() 点E点的坐标为(2,-1)
点E点的坐标为(2,-1)
当![]() 时,
时,![]()
 点E落在抛物线上.
点E落在抛物线上.
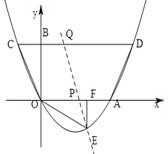
3.存在点P(a,0). 如上图记S梯形CQPO=S1,S梯形ADQP = S2,易求S梯形ABCD = 8.
当PQ经过点F(3,0)时,易求S1=5,S2 = 3,此时S1∶S2不符合条件,故a≠3.
设直线PQ的解析式为y = kx+b(k≠0),则![]() ,解得
,解得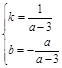 ,
,
∴![]() . 由y = 2得x = 3a-6,∴Q(3a-6,2)
. 由y = 2得x = 3a-6,∴Q(3a-6,2)
∴CQ = 3a-5,P O= a,![]() .
.
下面分两种情形:①当S1∶S2= 1∶3时,![]() = 2;
= 2;
∴4a-75= 2,解得![]() ;
;
②当S1∶S2= 3∶1时,![]() ; ∴4a-75= 6,解得
; ∴4a-75= 6,解得![]() ;
;
综上所述:所求点P的坐标为(![]() ,0)或(
,0)或(![]() ,0)
,0)
解析:(1)根据O、D两点的坐标求出抛物线的解析式,然后利用抛物线的性质求出C点的坐标;
(2)利用旋转、轴对称的性质求出E点的坐标,从而得出点E在抛物线上;
(3)分二种情况讨论:①梯形COPQ面积:梯形DAPQ面积=1:3,②梯形COPQ面积:梯形DAPQ面积=3:1.


科目:初中数学 来源: 题型:044
如图,抛物线![]() 经过原点,且对称轴在y轴的右侧与直线
经过原点,且对称轴在y轴的右侧与直线![]() 相交于M、N两点.
相交于M、N两点.
(1
)求m的值;(2
)求抛物线和直线的解析式;(3
)如果(2)中抛物线的对称轴与直线交于C点,与x轴交于B点,直线与x轴交于A点,P为抛物线对称轴上一动点,过点P作PD⊥AC,垂足为D.请问:点P分别在x轴上方或下方时,是否存在这样的位置,使
查看答案和解析>>
科目:初中数学 来源: 题型:
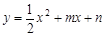 过原点O,与x轴交于A,点D(4,2)在该抛物线上,过点D作CD∥x轴,交抛物线于点C,交y轴于点B,连结CO、AD.
过原点O,与x轴交于A,点D(4,2)在该抛物线上,过点D作CD∥x轴,交抛物线于点C,交y轴于点B,连结CO、AD.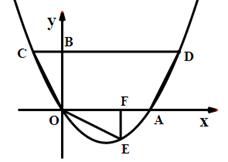
查看答案和解析>>
科目:初中数学 来源:2012届福建漳州中考模拟数学试卷(带解析) 题型:解答题
如图,抛物线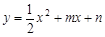 过原点O,与x轴交于A,点D(4,2)在该抛物线上,过点D作CD∥x轴,交抛物线于点C,交y轴于点B,连结CO、AD.
过原点O,与x轴交于A,点D(4,2)在该抛物线上,过点D作CD∥x轴,交抛物线于点C,交y轴于点B,连结CO、AD.
【小题1】求抛物线的解析式及点C的坐标
【小题2】将△BCO绕点O按顺时针旋转90°后 再沿x轴对折得到△OEF(点C与点E对应),判断点E是否落在抛物线上,并说明理由;
【小题3】设过点E的直线交OA于点P,交CD边于点Q. 问是否存在点P,使直线PQ分梯形AOCD的面积为1∶3两部分?若存在,求出P点坐标;若不存在,请说明理由.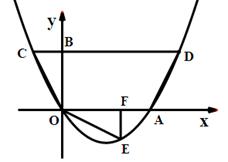
查看答案和解析>>
科目:初中数学 来源:2011-2012学年福建漳州中考模拟数学试卷(解析版) 题型:解答题
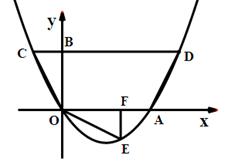
如图,抛物线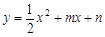 过原点O,与x轴交于A,点D(4,2)在该抛物线上,过点D作CD∥x轴,交抛物线于点C,交y轴于点B,连结CO、AD.
过原点O,与x轴交于A,点D(4,2)在该抛物线上,过点D作CD∥x轴,交抛物线于点C,交y轴于点B,连结CO、AD.
1.求抛物线的解析式及点C的坐标
2.将△BCO绕点O按顺时针旋转90°后 再沿x轴对折得到△OEF(点C与点E对应),判断点E是否落在抛物线上,并说明理由;
3.设过点E的直线交OA于点P,交CD边于点Q. 问是否存在点P,使直线PQ分梯形AOCD的面积为1∶3两部分?若存在,求出P点坐标;若不存在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com