
【题目】已知:如图,在矩形ABCD中,M,N分别是边AD,BC的中点,E,F分别是线段BM,CM的中点. 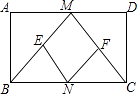
(1)求证:△ABM≌△DCM;
(2)判断四边形MENF是什么特殊四边形,并证明你的结论;
(3)当AD:AB=时,四边形MENF是正方形(只写结论,不需证明).
【答案】
(1)证明:∵四边形ABCD是矩形,
∴AB=CD,∠A=∠D=90°,
又∵M是AD的中点,
∴AM=DM.
在△ABM和△DCM中,
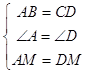 ,
,
∴△ABM≌△DCM(SAS)
(2)解:四边形MENF是菱形.
证明如下:
∵E,F,N分别是BM,CM,CB的中点,
∴NE∥MF,NE=MF.
∴四边形MENF是平行四边形.
由(1),得BM=CM,∴ME=MF.
∴四边形MENF是菱形
(3)2:1
【解析】(3)解:
当AD:AB=2:1时,四边形MENF是正方形.理由:
∵M为AD中点,
∴AD=2AM.
∵AD:AB=2:1,
∴AM=AB.
∵∠A=90,
∴∠ABM=∠AMB=45°.
同理∠DMC=45°,
∴∠EMF=180°﹣45°﹣45°=90°.
∵四边形MENF是菱形,
∴菱形MENF是正方形.
所以答案是:2:1.
【考点精析】利用菱形的判定方法和矩形的性质对题目进行判断即可得到答案,需要熟知任意一个四边形,四边相等成菱形;四边形的对角线,垂直互分是菱形.已知平行四边形,邻边相等叫菱形;两对角线若垂直,顺理成章为菱形;矩形的四个角都是直角,矩形的对角线相等.


科目:初中数学 来源: 题型:
【题目】如图,二次函数y=(x+2)2+m的图象与y轴交于点C,点B在抛物线上,且与点C关于抛物线的对称轴对称,已知一次函数y=kx+b的图象经过该二次函数图象上的点A(﹣1,0)及点B.
(1)求二次函数与一次函数的解析式;
(2)根据图象,写出满足(x+2)2+m≥kx+b的x的取值范围.

查看答案和解析>>
科目:初中数学 来源: 题型:
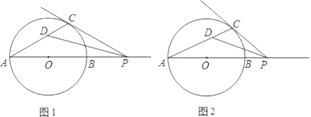
【题目】已知AB为⊙O的直径,P为AB延长线上的任意一点,过点P作⊙O的切线,切点为C,∠APC的平分线PD与AC交于点D.
(1)如图1,若∠CPA恰好等于30°,求∠CDP的度数;
(2)如图2,若点P位于(1)中不同的位置,(1)的结论是否仍然成立?说明你的理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
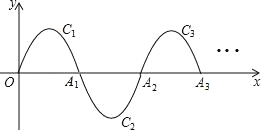
【题目】如图,一段抛物线:y=﹣x(x﹣2)(0≤x≤2)记为C1,它与x轴交于两点O,A1;将C1绕A1旋转180°得到C2,交x轴于A2;将C2绕A2旋转180°得到C3,交x轴于A3;…如此进行下去,直至得到C6,若点P(11,m)在第6段抛物线C6上,则m=_____.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com