Question

3．有甲、乙、丙三个村庄分别位于等边△ABC的顶点，在城中村改造时，为保护环境，改善居民的生活条件，政府决定铺设能够连结这三个村庄的天然气管道．设计人员给出了如图四个设计方案（点D为BC边的中点，点O为△ABC的中心，实线表示天然气管道），其中天然气管道总长最短的是（　　）

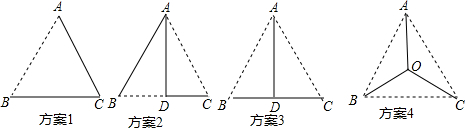
• A． 方案1
• B． 方案2
• C． 方案3
• D． 方案4

Answer 1

分析 认真观察图形，分别利用锐角三角函数关系得出4个方案的管道长度进而比较得出答案．

解答 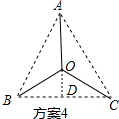解：设等边三角形的边长为a，
方案1：铺设路线的长为AB+AC=2a，
方案2：△ABC中的高线=AB•sin60°=$\frac{\sqrt{3}}{2}$a，故铺设路线的长度为AB+AD+DC=$\frac{3}{2}$a+$\frac{\sqrt{3}}{2}$a；
方案3：△ABC中的高线=AB•sin60°=$\frac{\sqrt{3}}{2}$a，故铺设路线的长度为BC+$\frac{\sqrt{3}}{2}$a=a+$\frac{\sqrt{3}}{2}$a；
方案4：如图所示：过点O作OD⊥BC于点D，
∵BD=$\frac{a}{2}$，
则BO=$\frac{\frac{a}{2}}{cos30°}$=$\frac{\sqrt{3}}{3}$a，
铺设路线的长为AO+BO+CO=3×$\frac{\sqrt{3}}{3}$a=$\sqrt{3}$a；
因为$\frac{3}{2}$a+$\frac{\sqrt{3}}{2}$a＞2a＞a+$\frac{\sqrt{3}}{2}$a＞$\sqrt{3}$a，所以方案4铺设路线最短．
故选D．

点评 本题考查了等边三角形的性质以及应用设计与作图；由于三角形内存在一点到三个顶点相等，所以类似最短路径问题，都涉及到三角形内这一点的运用．