
 ab+��a-b��2���ɴ��Ƶ�����Ҫ�Ĺ��ɶ�����a2+b2=c2��ͼ��Ϊ�����ڶ�ʮ����ͳ٤�ƶ��µġ���ͳ֤�������������֤����
ab+��a-b��2���ɴ��Ƶ�����Ҫ�Ĺ��ɶ�����a2+b2=c2��ͼ��Ϊ�����ڶ�ʮ����ͳ٤�ƶ��µġ���ͳ֤�������������֤���� ��a+b��2=
��a+b��2= ��a2+2ab+b2����
��a2+2ab+b2���� ab+
ab+ ba+
ba+ c2��
c2�� ��a2+2ab+b2��=
��a2+2ab+b2��= ��2ab+c2����
��2ab+c2���� a2+ab+
a2+ab+ b2=ab+
b2=ab+ c2��
c2��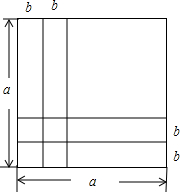


 ��ĩ1�����ʽ���������ϵ�д�
��ĩ1�����ʽ���������ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
| 1 | 2 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ��2011-2012ѧ�꽭��ʡ̫�������꼶���п�����ѧ������������ ���ͣ������
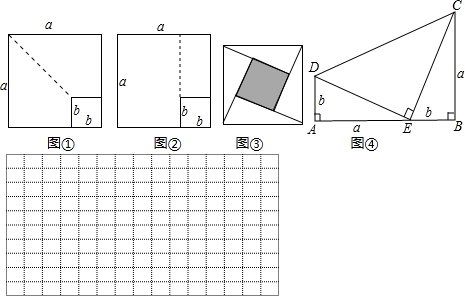
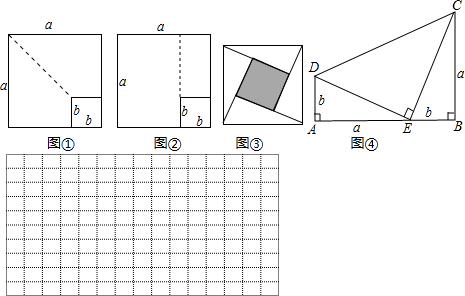
�̲ĵ�66ҳ̽��ƽ���ʽʱ�����������龳���߳�Ϊb��С������ֽƬ�����ڱ߳�Ϊa�Ĵ�������ֽƬ�ϣ���ͼ9?6��������ͨ������δ��ס���ֵ�����õ���ʽ(a + b) (a?b) = a2?b2�𣿣�����֤����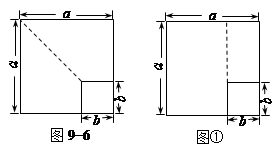
(1)�����С�����ε�һ���ӳ�����ͼ�٣����Ƿ�Ҳ���Ƶ���ʽ�������֤����
(2) ��������˿��������Ǽ��乫ʽ��������ֱ�۵��Ƶ�����֤��ʽ���׳ơ�����֤���������磬��������ˬ��ͼ����ͼ�ڣ������ĸ�ֱ�������νϴ��ֱ�DZ߳���Ϊa����С��ֱ�DZ߳���Ϊb��б�߳���Ϊc�����������ε�������Ա�ʾΪc2��Ҳ���Ա�ʾΪ4´ ab + (a ?b)2���ɴ��Ƶ�����Ҫ�Ĺ��ɶ�����a2 + b2 = c2��ͼ��Ϊ�����ڶ�ʮ����ͳ٤�ƶ��µġ���ͳ֤�������������֤����
ab + (a ?b)2���ɴ��Ƶ�����Ҫ�Ĺ��ɶ�����a2 + b2 = c2��ͼ��Ϊ�����ڶ�ʮ����ͳ٤�ƶ��µġ���ͳ֤�������������֤����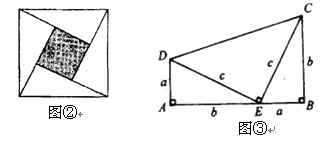
(3) �Թ���һ��ͼ�Σ�ʹ��������ܹ�����(a? 2b)2 = a2?4ab + 4b2����������ĸ���У��������ĸa��b����ʾ���߶Σ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ��2011-2012ѧ�꽭��ʡ̫�������꼶��ѧ�����п�����ѧ�Ծ����������� ���ͣ������
�̲ĵ�66ҳ̽��ƽ���ʽʱ�����������龳���߳�Ϊb��С������ֽƬ�����ڱ߳�Ϊa��
��������ֽƬ�ϣ���ͼ9?6��������ͨ������δ��ס���ֵ�����õ���ʽ(a + b) (a ? b) = a2? b2��
������֤����
(1)�����С�����ε�һ���ӳ�����ͼ�٣����Ƿ�Ҳ���Ƶ���ʽ�������֤����
(2) ��������˿��������Ǽ��乫ʽ��������ֱ�۵��Ƶ�����֤��ʽ���׳ơ�����֤���������磬��������ˬ��ͼ����ͼ�ڣ������ĸ�ֱ�������νϴ��ֱ�DZ߳���Ϊa����С��ֱ�DZ߳���Ϊb��б�߳���Ϊc�����������ε�������Ա�ʾΪc2��Ҳ���Ա�ʾΪ4´ ab + (a ? b)2���ɴ��Ƶ�����Ҫ�Ĺ��ɶ�����a2 + b2 = c2��
ab + (a ? b)2���ɴ��Ƶ�����Ҫ�Ĺ��ɶ�����a2 + b2 = c2��
ͼ��Ϊ�����ڶ�ʮ����ͳ٤�ƶ��µġ���ͳ֤�������������֤����

(3) �Թ���һ��ͼ�Σ�ʹ��������ܹ�����(a ? 2b)2 = a2? 4ab + 4b2����������ĸ���У��������ĸa��b����ʾ���߶Σ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ��2014�콭��ʡ̫�������꼶��ѧ�����п�����ѧ�Ծ��������棩 ���ͣ������
�̲ĵ�66ҳ̽��ƽ���ʽʱ�����������龳���߳�Ϊb��С������ֽƬ�����ڱ߳�Ϊa��
��������ֽƬ�ϣ���ͼ9−6��������ͨ������δ��ס���ֵ�����õ���ʽ(a + b) (a − b) = a2 − b2��
������֤����
(1)�����С�����ε�һ���ӳ�����ͼ�٣����Ƿ�Ҳ���Ƶ���ʽ�������֤����

(2) ��������˿��������Ǽ��乫ʽ��������ֱ�۵��Ƶ�����֤��ʽ���׳ơ�����֤���������磬��������ˬ��ͼ����ͼ�ڣ������ĸ�ֱ�������νϴ��ֱ�DZ߳���Ϊa����С��ֱ�DZ߳���Ϊb��б�߳���Ϊc�����������ε�������Ա�ʾΪc2��Ҳ���Ա�ʾΪ4´ ab
+ (a − b)2���ɴ��Ƶ�����Ҫ�Ĺ��ɶ�����a2 +
b2 = c2��
ab
+ (a − b)2���ɴ��Ƶ�����Ҫ�Ĺ��ɶ�����a2 +
b2 = c2��
ͼ��Ϊ�����ڶ�ʮ����ͳ٤�ƶ��µġ���ͳ֤�������������֤����


(3) �Թ���һ��ͼ�Σ�ʹ��������ܹ�����(a − 2b)2 = a2 − 4ab + 4b2����������ĸ���У��������ĸa��b����ʾ���߶Σ�

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ��2014�콭��ʡ̫�������꼶���п�����ѧ���������棩 ���ͣ������
�̲ĵ�66ҳ̽��ƽ���ʽʱ�����������龳���߳�Ϊb��С������ֽƬ�����ڱ߳�Ϊa�Ĵ�������ֽƬ�ϣ���ͼ9−6��������ͨ������δ��ס���ֵ�����õ���ʽ(a + b) (a − b) = a2 − b2�𣿣�����֤����

(1)�����С�����ε�һ���ӳ�����ͼ�٣����Ƿ�Ҳ���Ƶ���ʽ�������֤����
(2) ��������˿��������Ǽ��乫ʽ��������ֱ�۵��Ƶ�����֤��ʽ���׳ơ�����֤���������磬��������ˬ��ͼ����ͼ�ڣ������ĸ�ֱ�������νϴ��ֱ�DZ߳���Ϊa����С��ֱ�DZ߳���Ϊb��б�߳���Ϊc�����������ε�������Ա�ʾΪc2��Ҳ���Ա�ʾΪ4´ ab + (a − b)2���ɴ��Ƶ�����Ҫ�Ĺ��ɶ�����a2 + b2
= c2��ͼ��Ϊ�����ڶ�ʮ����ͳ٤�ƶ��µġ���ͳ֤�������������֤����
ab + (a − b)2���ɴ��Ƶ�����Ҫ�Ĺ��ɶ�����a2 + b2
= c2��ͼ��Ϊ�����ڶ�ʮ����ͳ٤�ƶ��µġ���ͳ֤�������������֤����

(3) �Թ���һ��ͼ�Σ�ʹ��������ܹ�����(a − 2b)2 = a2 − 4ab + 4b2����������ĸ���У��������ĸa��b����ʾ���߶Σ�

�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com