Question

如图，AB为量角器（半圆O）的直径，等腰直角△BCD的斜边BD交量角器边缘于点G，直角边CD切量角器于读数为60°的点E处（即弧AE的度数为60°），第三边交量角器边缘于点F处．
 
（1）求量角器在点G处的读数α（0°＜α＜90°）；
（2）若AB=10cm，求阴影部分面积．

Answer 1

（1）30°  ；（2）－

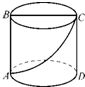
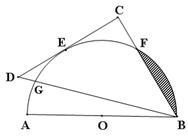
试题分析：（1）连接OE，OF，先根据切线的性质可得OE⊥CD，再根据BD为等腰直角△BCD的斜边，可得BC⊥CD，∠D=∠CBD=45°，即可证得OE∥BC，则有∠ABC=∠AOE=60°，即得∠ABG的度数，从而可以求得结果；
（2）先证得△OBF为正三角形，先根据阴影部分的面积等于扇形OBF的面积-三角形OBF的面积，结合扇形的面积公式及三角形的面积公式求解即可.
（1）连接OE，OF

∵CD切半圆O于点E
∴OE⊥CD，
∵BD为等腰直角△BCD的斜边，
∴BC⊥CD，∠D=∠CBD=45°，
∴OE∥BC
∴∠ABC=∠AOE=60°，
∴∠ABG=∠ABC-∠CBD=60°-45°=15°
∴弧AG的度数=2∠ABG=30°，
∴量角器在点G处的读数α=弧AG的度数=30°  ；
（2）∵OF=OB=0.5AB=5cm，∠ABC=60°，
∴△OBF为正三角形，∠BOF=60°，
∴S_扇形=（cm²），S_△OBF=
∴S_阴影=S_扇形-S_△OBF=－
点评：本题知识点较多，综合性较强，是中考常见题，熟练掌握圆的相关性质是解题关键.