
分析 (1)利用根与系数的关系得出x1+x2=-4,x1•x2=-2,进一步整理代入求得数值即可;
(2)利用根与系数的关系直接求得答案即可;
(3)利用两个实数根互为倒数得出m2-3=1,求得m的数值,进一步判断得出答案即可.
解答 解:(1)∵x1+x2=-4,x1•x2=-2,
∴$\frac{1}{x_1}+\frac{1}{x_2}=\frac{{{x_1}+{x_2}}}{{{x_1}{x_2}}}$=2.
(2)$b=-(\sqrt{2}+1+\sqrt{2}-1)$=$-2\sqrt{2}$,$c=(\sqrt{2}+1)(\sqrt{2}-1)$=1;
(3)∵m2-3=1,
∴m=±2(2分),
当m=2时,方程没有实数根,舍去,
当m=-2时,方程有两个实数根互为倒数.
点评 本题考查了根与系数的关系:若x1,x2是一元二次方程ax2+bx+c=0(a≠0)的两根时,x1+x2=-$\frac{b}{a}$,x1x2=$\frac{c}{a}$.


 全优考典单元检测卷及归类总复习系列答案
全优考典单元检测卷及归类总复习系列答案 品学双优卷系列答案
品学双优卷系列答案 小学期末冲刺100分系列答案
小学期末冲刺100分系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
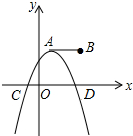 如图,点A,B的坐标分别为(1,3)和(5,3),抛物线y=a(x-h)2+k的顶点在线段AB上运动,与x轴交于C、D两点(C在D的左侧),点C的横坐标最小值为-3,则点D的横坐标最大值为9.
如图,点A,B的坐标分别为(1,3)和(5,3),抛物线y=a(x-h)2+k的顶点在线段AB上运动,与x轴交于C、D两点(C在D的左侧),点C的横坐标最小值为-3,则点D的横坐标最大值为9.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com