练习册

  • 练习册
  • 试题
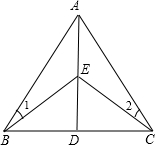    精英家教网 > 初中数学 > 题目详情
    已知：如图，AD是三角形纸片BC边上的高．将纸片沿直线EF折叠，使点A和点D重合．求证：EF∥BC．
    分析：根据翻折变换的性质得出EF⊥AD，进而利用平行线的判定得出即可．
    解答：证明：∵AD是三角形纸片BC边上的高．将纸片沿直线EF折叠，使点A和点D重合，
    ∴EF⊥AD，AQ=QD，
    ∴∠AQE=∠ADB=90°，
    ∴EF∥BC．
    点评：此题主要考查了翻折变换的性质，根据已知得出EF⊥AD是解题关键．
    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    精英家教网已知：如图，D是△ABC中BC边上一点，E是AD上的一点，EB=EC，∠1=∠2．
    求证：AD平分∠BAC．
    证明：在△AEB和△AEC中，
    EB=EC
    ∠1=∠2
    AE=AE

    ∴△AEB≌△AEC（第一步）
    ∴∠BAE=∠CAE（第二步）
    ∴AD平分∠BAC（第三步）
    问：上面证明过程是否正确？若正确，请写出题中标出的每一步推理根据；若不正确，请指出错在哪一步？并写出你认为正确的推理过程．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    （2013•闵行区三模）已知：如图，△ABC是等边三角形，点D在边BC上，且△ADE是等边三角形．过点E作EF∥BC，EF分别与线段AB、AC、AD相交于点F、G、H，联结CE．
    （1）求证：四边形BCEF是平行四边形；
    （2）如果AD⊥BC，求证：BC=2FG．

    查看答案和解析>>

    科目：初中数学 来源：2012届湖北省宜昌市长阳县九年级上学期期末复习数学试卷（带解析） 题型：解答题

    已知：如图，D是△ABC中BC边上一点，E是AD上的一点， EB=EC，∠1=∠2．

    求证：AD平分∠BAC．
    证明：在△AEB和△AEC中，

    ∴△AEB≌△AEC（第一步）
    ∴∠BAE="∠CAE" （第二步）
    ∴ AD平分∠BAC（第三步）
    问：上面证明过程是否正确？若正确，请写出题中标出的每一步推理根据；若不正确，请指出错在哪一步？并写出你认为正确的推理过程．

    查看答案和解析>>

    科目：初中数学 来源：2011-2012学年湖北省宜昌市长阳县九年级上学期期末复习数学试卷（解析版） 题型：解答题

    已知：如图，D是△ABC中BC边上一点，E是AD上的一点， EB=EC，∠1=∠2．

    求证：AD平分∠BAC．

    证明：在△AEB和△AEC中，

    ∴△AEB≌△AEC（第一步）

    ∴∠BAE=∠CAE （第二步）

    ∴ AD平分∠BAC（第三步）

    问：上面证明过程是否正确？若正确，请写出题中标出的每一步推理根据；若不正确，请指出错在哪一步？并写出你认为正确的推理过程．

     

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    已知：如图，D是△ABC中BC边上一点，E是AD上的一点， EB=EC，∠1=∠2．

    求证：AD平分∠BAC．

    证明：在△AEB和△AEC中，

    ∴△AEB≌△AEC（第一步）

    ∴∠BAE=∠CAE （第二步）

    ∴ AD平分∠BAC（第三步）

    问：上面证明过程是否正确？若正确，请写出题中标出的每一步推理根据；若不正确，请指出错在哪一步？并写出你认为正确的推理过程．

     


    查看答案和解析>>

    同步练习册答案