
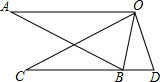
 如图,△ABO≌△CDO,点B在CD上,AO∥CD,∠BOD=30°,则∠A=30°.
如图,△ABO≌△CDO,点B在CD上,AO∥CD,∠BOD=30°,则∠A=30°. 科目:初中数学 来源: 题型:解答题
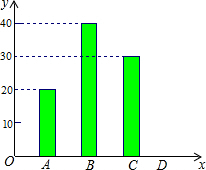 “五•一”假期,某公司组织部分员工分别到A、B、C、D四地旅游,公司按定额购买了前往各地的车票.如图是未制作完的车票种类和数量的条形统计图,根据统计图回答下列问题:
“五•一”假期,某公司组织部分员工分别到A、B、C、D四地旅游,公司按定额购买了前往各地的车票.如图是未制作完的车票种类和数量的条形统计图,根据统计图回答下列问题:查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com